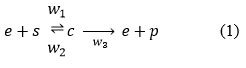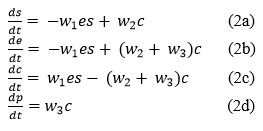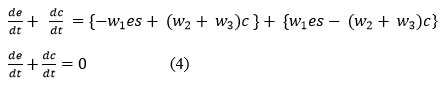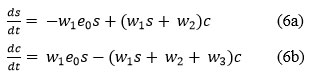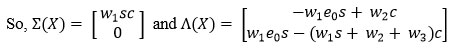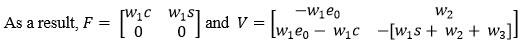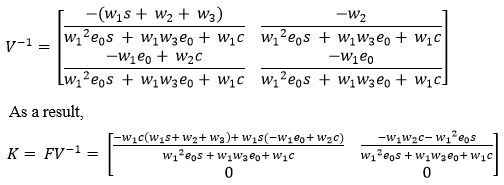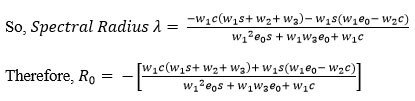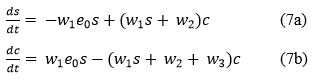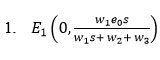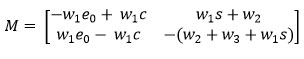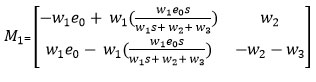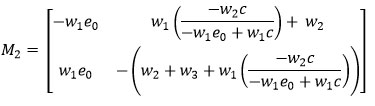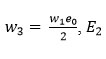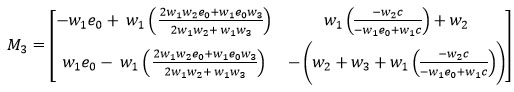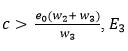Introduction

Most of the chemical transformations inside the cell carry proteins called enzymes. Enzymes (BIOCATALYSTS) act upon molecules called Substrates to generate products rapidly, (reversible) deprived of being absorbed during the procedure. The whole enzyme molecule is not active in catalyzing a chemical reaction. Only its active site is active. Enzymes are well-defined by their kinetic behavior of binding with the substrate for product formation, which is much more alluring.^1,2

Examining the kinetics enzyme is critical for understanding cellular systems and enzymes in industry. This is introduced in the books by using a mathematical curve namely, Rubinow,³ Murray,⁴ Segel,⁵ and Roberts.⁶ In particular, Kinesiology of Enzymes have been deeply subject to the paradigm of biological processes proposed by Henri,^7,8,9 the canonical approach by Michaelis and Menten,¹⁰ and further developed by Briggs and Haldane through Bayesian approach based on the total quasi-steady-state approximation.¹¹

Various simplified analytical Solutions of the model use the techniques, such as Homotopy Perturbation Technique, Variational Iteration Technique, Laplace Transform (LT), Danckwort’s expression, and He’s variation iteration method.^12,13,14 Numerical solutions of the model are also based on the Finite Difference Technique, HPM, HAM, VIM, ADM,^15,16,17,18 etc.

In order to cope with the exact theatrical solution for the enzymatic reaction. The analysis aims to study the effect of enzymes on substrates for the formation of the product. Formulate the normalized model as a system of nonlinear differential equations. Compute the threshold value to study the effect of enzyme, complex, and other parameters on the substrate for product formation. The aim is to perform the stability analysis for ideal product formation hence, the need for asymptotically stable solutions to the given model with simulation. The perseverance of this work is to derive the numerical solution of the system with convergence criteria along with the stability analysis. The use of the Next Generation Matrix method and calculation of the reproduction number for the stability of our model is proceeded by the existence of possible equilibrium points with their restrictions, followed by sensitive analysis using all possible parametric values. We derive asymptotically stable solutions to the model with simulation.

Mathematical Model Formulation

The mathematical formulation of the enzyme kinematics problem in biochemical systems has been modeled using ordinary differential equations. The enzyme binds to the substrate to generate an enzyme-substrate complex. Which then releases the product and independent enzyme. The independent enzyme is then available for a different reaction to produce a new substrate. Thus the system is written as:

The fundamental enzymatic reaction:

Where; s=[s], e=[e], c=[c]and p=[p] are their normalized concentrations in 1 mg.

This procedure demonstrates the binding of substrate s and the discharge of product p. e is the independent enzyme and c is the enzyme-substrate complex w₁, w₂ and w₃ are the weight representing the reaction of three processes. It is to be ensure that substrate binding is reversible but product release is not. This chemical reaction, can be converted to a mathematical model using the mass action law and favorable analysis, the system of non-linear reaction equations is represented as follows:¹⁴ 

Where w₁ is the weight of the positive rate of  forming complex, w₂ is the weight of the reverse(negative) rate constant, w₃ is the rate of product formation and enzyme release, and c is the complex intermediate species.

Consider the normalized initial conditions for substrate s enzyme e , complex c, and product p as follows:

Where, equation (2d) is directly integrable, and equations (2b, 2c) are reciprocal of each other.

So, adding equations (2b) and (2c),

Also, the initial conditions in equation (3) state that,

hence, the system of ordinary differential equations reduces, for s and c,¹⁴ namely

Where substrate s and complex c has normalized initial conditions s(0) = s₀  and c(0) = 0.

The stability of this System

Theorem: A system of a differential equation is asymptotically stable if and only if its basic reproduction number (R₀)  is not more than or equal to 1.

To determine (R₀) using Next Generation Matrix.  is next generation matrix, where F and V both are Jacobian of Σ and Λ evaluated for Enzyme, Substrate, and Complex at an equilibrium point.^19,20,21

Where, X =(s, c)^t, Σ(X) denotes the entrance to the compartment and Λ(X) denotes transferring to another compartment or leaving the system. Then the Jacobian at the equilibrium point is given by

Theorem: If the determinant of a matrix is non-zero then its inverse does exist.

The basic reproduction number is defined as the magnitude of the largest eigenvalue of the matrix K. which is the spectral radius.

Consequently, for all possible positive parametric values, R₀ of our system is less than 1. Hence the system is asymptotically Stable.

Boundedness / Existence of solution

Theorem: Let D ⊆ R × Rⁿ be a closed rectangle with (t_0, z₀)∈ D . Let f😀→ Rⁿ  be a function being continuous in t and Lipchitz Continuous in y. Then, there exists positive  where the IVP zⁱ(t) = f(t,z(t)),z(t_o)= z_o. has  single solution z(t) on the interval [ t₀ – e_, t₀ + e ]

The mathematical model of our arrangement is well established. In fact, it has single solution existence and constantly depends on the output data. Since we are dealing with the humanoid inhabitants, we must ensure that our solutions are positive and bound.¹⁸

Equilibrium Point and their existence

solving the algebraic equations(7a) and (7b), the equilibrium points of System are defined to be.

There are three equilibrium points:

exists provided the following conditions are satisfied: w₁s + w₂ + w₃ ≠ 0

exists provided the following conditions are satisfied: w₁ e₀ + w₁c ≠ 0

exists provided the following conditions are satisfied: 2w₁ w₂ + w₁w₃ ≠ 0 and w₁ e₀ + w₁c ≠ 0

Stability Analysis

The local stability behaviour of equilibrium points is determined by eigenvalues of corresponding Jacobian Matrix.^22,23,24,25

Theorem: If all the Eigenvalues of a n ×n  matrix are negative,(values being real) then the equilibrium point is asymptotically stable.

Theorem: If the real part of all the Eigenvalues of a n ×n matrix are negative, (values being complex) then the equilibrium point is asymptotically stable.

The general Jacobian Matrix M for our model (7a) and (7b) is given as:

Let M_i, Where i=1,2 & 3 be the matrix evaluated at the equilibrium point  where .

Then the matrix M₁ evaluated at the equilibrium E₁ is represented as follows:

Since, the matrix M₁ has negative Eigen values under the condition , is a stable equilibrium point.

Again, the matrix M₂ calculated at the equilibrium E₂ is characterized as follows:

As the matrix M₂ contributes the negative real part of its complex Eigen values under the condition:

is a stable equilibrium point.

Now, M₃ be the matrix evaluated at the equilibrium E₃ is symbolized as follows: 

Since, the matrix M₃ contributes the negative real part of its complex Eigen values under the condition: 

is a stable equilibrium point.

Sensitive Analysis

On considering the initial conditions to be equal (e(0)=s(0) =1 mg) the corresponding parametric values are measured as follows:

Table 1: Value of the model parameters in enzymatic reaction for product formation

The ranking is provided as per the time consumption for product formation. Keeping parameter w₁ constant, parameter w₂ smaller than w₁ and w₃ bigger than w₁ than the time consumption for product formation is minimum so it is ranked 1. Making parameter w₃ constant with w₂ bigger and w₃ smaller turns up to maximum time consumption and hence ranked 5. Similarly, other possibilities are ranked accordingly. It is important to note down that taking any parametric values to be non – positive, it results to the failure. 

Result and Discussion

Since minimum time consumption for product formation is on keeping the parameters to be fixed at w_{1 =} 2, w_{2 =} 1, w_{3 =} 3. The change in enzyme and substrate concentration is studied for this hypothesis as follows:

Figure 1: Time – Concentration relation   Click here to view figure

The initial concentration of both enzyme and substrate is taken to be equal (e(0) = s(0) = 1 mg).

Figure 2: Time – concentration relation   Click here to view figure

The initial concentration of enzyme is less than that of substrate (e(0) = 0.8 mg and s(0) = 1 mg).

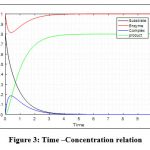Figure 3: Time –Concentration relation   Click here to view figure

The initial concentration of enzyme is more than that of substrate (e(0) = 1 mg and s(0) = 0.8 mg).

It is noted that, while compelling concentration of enzyme to be smaller than that of substrate (e(0) = 0.8 mg and s(0) = 1 mg) then constant product formation is after 5 seconds. And if concentration of enzyme and substrate both equal (e(0) = s(0) = 1 mg) then constant product formation is later 4 seconds. Wheras for concentration of enzyme to be more than that of substrate (e(0) = 1 mg and s(0) = 0.8 mg) then again time consumption is more than 4 seconds.      

Conclusions

In this paper, it is revealed that the experimentally observed enzyme–substrate relationship is consistent with theatrical calculations. Using the parametric values from the graph, the Reproduction Number is calculated as -0.4 which is the threshold value for product formation. Further the stability analysis carried out with constant initial conditions stated that, variation in rate of constants w₁, w₂  and w₃ do affects the time consumption for product formation. It is inferred that w₁ < w₂ < w₃ consumes the minimum time span for product formation whereas w₁ < w₂ < w₃ takes the maximum time for the same. Also, it is observed that taking any of the parametric value to be negative tends to the failure of product formation. On applying restrictions to the initial conditions, it is inferred that enzyme concentration must be more than or at least equal to the substrate concentration, for ideal product formation. Whereas, the concentration of enzyme to be less than that of substrate consumes more time for product formation.

Acknowledgement

The authors are thankful to anonymous referees for their valuable suggestions and comments to improve this manuscript.

Conflict of interest

The authors declare that there is no conflict of interest involved in this study.

Funding sources

The authors received no external funding support for this research work.

References

1. James K. and James S. Mathematical Physiology- cellular physiology. 2008; Vol 8/I, 1: 07-15.
2. Bhatia K.N. and Tyagi M.P. Elementary Biology,A Trueman Publication, latest edition; Vol I: U3: 90 – 104.
3. Rubinow S.I., Introduction to Mathematical Biology. Wiley, Newyork, 1975.
4. Murray J.D., Mathematical Biology. Springer, Berlin, 1989.
   CrossRef
5. Segel L.A., Mathematical Models in Molecular and Cellular Biology. Cambridge University Press, Cambridge. 1980.
6. Roberts D.V., Enzyme Kinetics. Cambridge University Press, Cambridge. 1977
7. Henri V., Recherches sur la loi de l’action de la sucrase. C. R. Hebd. Acad. Sci. 1901a.; 133:891– 899.
8. Henri, V., Uber das gesetz der wirkung des invertins. Z. Phys. Chem. 1901b.; 39:194–216.
   CrossRef
9. Henri, V., Theorie g ´ en´ erale de l’action de quelques diastases. C. R. Hebd. Acad. Sci. 1902; 916–919.
10. Michaelis, L., and Menten, M.L., Die kinetik der invertinwirkung. 1913.
11. Briggs G.E. and Haldane J.B.S. A note on the kinetics of enzyme action. J. Biochem., 1925; 19: 338– 339.
    CrossRef
12. Rahamathunissa G. and Rajendran L. Modeling of Nonlinear Reaction – Diffusion Processes of Amperometric Polymer- Modified Electrodes. Journal Mathematical Chemistry, 2008; 44: 849–801.
    CrossRef
13. Rajendran L., Mohan C., Fernandez C.M. and Peng Q. Mathematical Modelling and Simulation of Nonlinear Process in Enzyme Kinetics. Intechopen, 2018.
    CrossRef
14. Leyla N. A. Some comments on enzyme kinetics studies. Turkish J. Biochem., 2020.
15. Hugo D., Matteo M, Terence H., and Martin J. L. On the optimality of the enzyme–substrate relationship in bacteria. PLOS BIOLOGY, 2021.
16. Alyssa C. Enzyme Deficiencies and its Causes, 2022; Volume 11, Issue 2.
17. Khan M, Ahmad Z, Ali F, Khan N, Khan I, and Kottakkaran S. N. Dynamics of two-step reversible enzymatic reaction under fractional derivative with Mittag-Leffler Kernel. PLOS ONE, 2023.
    CrossRef
18. Meena, A., Eswari, A. and Rajendran, L. Mathematical modelling of enzyme kinetics reaction mechanisms and analytical solutions of non-linear reaction equations. J Math Chem, 2010; 48: 179–186.
    CrossRef
19. Ismail I, Oluleye G, and Oluwafemi IJ, et al. Mathematical modelling of an enzyme-based biosensor. Int J Biosen Bioelectron., 2017;3(2):265–268.
    CrossRef
20. Fantaye A.K., Goshu M.D., Zeleke B.B., Gessesse A.A., Endalew M.F. and Birhanu Z.K. Mathematical model and stability analysis on the transmission dynamics of skin sores. Epidemiol Infect., 2022;150: 1-9.
    CrossRef
21. Jones J. H. Notes On RStanford University, 2007.
22. Hai-Fenf Huo and Li-Xiang Feng. Global stability of an Epidemic Model with Incomplete Treatment and Vaccination. Hindawi Publishing Corp., 2012.
    CrossRef
23. Daniel E. E., Daniel O. E., Ibrahim I. A., and Adamu M. U. STABILITY ANALYSIS ON SIR AND SIS COMPARTMENTAL EPIDEMIOLOGICAL MODELS. ftst journal, 2021; 6: 289 – 295.
24. James A. A., and Babatunde S. O. Boundedness and Stability Properties of Solutions of Mathematical Model of Measles. Tamkang Journal of Mathematics, 2021; 52: 91-112.
    CrossRef
25. Joko H., and Titik S. Local Stability Analysis of an SVIR Epidemic Model, Jurnal Matematika Murni dan Aplikasi, 2017; 5: 20-28.
    CrossRef