Introduction

The need for digital image processing stems from two primary areas of applications: improvement in the pictorial quality of an image for increased human perception; and secondly to process image data to make it suitable for storage, transmission and representation for direct machine perception. An image is a two dimensional signal, the spatial coordinates at any point defines the discrete pixel intensity value at that any point in the image.

In case of colour images, a pixel value at location (i,j) are represented by three intensity values each corresponding to red, blue and green colours respectively. It can also be referred to as the extraction of the useful information from the image with the help of computer algorithms. A digital processing task can be broadly divided into three categories: Image Acquisition- to map the object or view in to 2-dimensional format to make it suitable for storage, transmission and processing; Image processing: improving the quality of degraded image with help of image enhancement and image restoration; Image analysis: to analyse the image for feature extraction and object recognition [Elad et al 2006, Mihcak et al 1999].

These days there is no such area which has not been influenced by the field of image processing. The broad areas of applications of image processing are as follows  [Ghanekar et al 2010, Ghanekar et al 2007, Chambolle 2004]:

Natural Imaging: used in multi-media tools and applications.

Medical Sciences: medical imaging modalities like CT, MRI, SPECT and DSA are used for diagnosis of various ailments.

Biometrics and Forensics: Classifying the physical characteristics of face, fingerprints, iris and palm for identification.

Remote Sensing and Satellite imaging: Images acquired from remote areas and satellites finding application in weather forecasting, determines local terrains of mountains, locating natural resources like water and forests.

Traffic Control: Monitoring and assessment of pictures for traffic control.

Industrial and Agricultural Automation: Automated visual inspection in aerospace, textiles, food and crop industry.

Defence and military surveillance: Infrared and visible imaging is employed to for surveillance e.g., Night vision devices.

Image Denoising

The numerous applications of a digital image, makes it imperative for them to visual informative and suitable for further image processing applications. Elimination of noise is an elementary step in any image analysis task which ranges from simple enhancement of image to more complex functions like feature extraction.

A degraded image impedes the process of automated image processing. The efficient image representation plays a vital role in pattern recognition and design of computer aided tools. Properly denoised image can act as an effective input source for further image processing tasks like biometrics, medical imaging, surveillance, remote sensing and defence application. As the design of high resolution of cameras continues, so is the susceptibility to sensor noise. This gives rise to the requirement of effectual denoising algorithms. Noise can occur over transmission medium due to a noisy channel, errors during the measurement process and during quantization of the data for digital storage. Noise is uncorrelated amongst pixels, i.e. there is no relation between the pixel values and the values of the noise components.

A Model of the Image Degradation/Restoration Process

The typical denoising model for an input image can be assumed as given in Fig. 1.1. The given input function (image) is f (a,b). A degradation function H operates on f (x,y), along with additive noise. Given some knowledge about the degradation function and some knowledge about noise n (a,b) the objective of this model is to obtain the closest possible estimate ƒ (x,y) or F(a,b) of the original image. H is usually a linear position invariant process, then the degraded image in the spatial domain is given by g (a,b) =h(a,b) ∗ f (a,b) + n(a,b) where h (a,b) is the spatial domain representation of the degradation function and the symbol ∗ indicates convolution. The equivalent representation in the frequency domain can be given as:

G (u,v) =H(u,v) F(u,v) + N(u,v)

where the terms in capital letters denote the Fourier transforms of the corresponding terms in spatial domain. The following model forms the basis of any fundamental to highly complex denoising algorithm [6].

Figure 1.1: Image Denoising process [Gonzalez et al 2007]   Click here to View figure

Types of Noise

Noise is an arbitrary variation in the local information of the image like brightness and colour information and is usually electronic in nature. The fairly common types of noises are Additive White Gaussian Noise (AWGN), Poisson Noise (shot noise), Impulse noise, Speckle noise and Quantization noise (uniform noise). One of the most occurring noises in images is Gaussian noise [Verma et al 2013]. The ecological surroundings while image acquisition and the quality of the imaging sensor elements affect their performance resulting in degraded image quality. For instance, while capturing the images via CCD (charged coupled device) cameras, the levels of light and the temperature of the sensors are one of the major factors contributing to the presence of noise in the resultant image. Besides this images are contaminated with noise due to interference in the transmission channel. An image passed on over a wireless network could be contaminated with lightening or some other types of atmospheric turbulences. Some types of noises can be present in the images due to poor illumination in the image capturing vicinity, due to insufficient photon count or faulty memory location [Zhu et al 2009].

Gaussian Noise         

The primary sources of Gaussian noise happen during image capturing i.e. sensor noise caused by the intrinsic thermal and electronic fluctuations of the acquisition devices. Gaussian noise exhibits a noise model having probability density function (PDF) which is normally distributed. The values of noise are Gaussian-distributed with known variance and zero mean. The primary source of Gaussian noise is due thermal energy of the electrons in the electronic transmission channels. Where the level of illumination and the temperature of the sensor also contribute to amount of Gaussian noise, the electronic circuits connected to the imaging sensors inject their own share of electronic circuit noise. The Gaussian noise is additive in nature and independent of the pixel intensity. It is generally called thermal noise (John-Nyquist noise) which arises from the reset noise of capacitors [Moulin et al 1999].

Impulse Noise

In case of impulse noise the pixels corrupted with pepper noise (dark pixels) has got 0 as intensity value and pixels corrupted with salt noise (white pixels) have pixel intensity value as 1. The major sources of this are bit errors in transmission and analog-to-digital convertors [Chan 2005].

Poisson Noise

Due statistical quantum fluctuations, there is a typical kind of noise which arises due to variation in the number of photons sensed at a certain exposure level and is known as photon shot noise. This type of noise generally follows Poisson distribution; however at lower levels it tends to follow Gaussian distribution. In PDF of Poisson noise, the mean and variance are nearly equal and the signal-to-noise ratio at n^th pixel is signal dependent and spatially varying.  It usually manifests itself in the darker regions of the image due to statistical quantum fluctuations [Kuan 1985].

Quantization Noise

Another type of noise called Quantization noise approximately displays uniform distribution and also known as uniform noise. Quantization means sampling, hence it is caused during the sampling of the captured pixels of an image. Though it can be signal dependent, but if wavering is explicitly applied it will be signal independent [Watson et al 1997].

Major Issues in the Domain of Image Denoising

The removal of noise is one most fundamental and classical problem in image processing and computer vision which holds substantial practical importance for real-world applications. Image denoising is a common denominator of all imaging systems and it enables the realization of the basic understanding of characteristics of an image. Image noise suppression is an important task which forms the basis any more complex higher level applications like, satellite television, geographical information systems, astronomy and medical imaging [Rajwade et al 2012]. Besides this is an important pre-processing step for further image analysis. The noise manifests itself in a random uncorrelated manner leading to the degradation of the quality of vital data. The software solutions are more preferred than optical hardware solutions, as they the former is device independent. Image denoising is not only important for visual image enhancement but to facilitate the further automated processing of the image [Shao et al 2014].

An image corrupted with noise makes it challenging for the user to comprehend or acquire the desired information. In the field of medical image analysis the image contaminated with noise can highly disrupt the diagnosis process and cause serious damage to the patient care and treatment.  Noisy images become either useless for image processing tasks like image fusion, image registration or requires a huge amount of effort and time to make them fit for further use. In context of remote sensing images the clarity of images play a major role in locating various geographical points or to state the position, topography etc. of the area captured by a camera.

Furthermore it was found that most of the types of noises affect the edges and boundaries of the images which destroy the important structural information which is vital for computer aided data applications. Hence there emerges an increasing need to denoise the image to make it fit for proper data processing and application.

The researchers continuously thrive to design image denoising algorithms, which have achieved optimal performance. The process of image denoising can be conducted using methods which can broadly be categorised into four categories: Spatial domain methods; transform domain methods; dictionary learning methods and newly worked upon hybrid domain methods.

In the field of denoising one can either exploit the spatial domain filters, can work with filters in frequency domain and can also rely on dictionary learning methods. Spatial domain methods include local and non local filters edge preserving filters which are based on the correlation amongst pixels. The Gaussian filter, Anisotropic Diffusion filter, SUSAN filter, Bilateral Filter, Non-local Mean Filter are some of the common spatial domain filters (Yu et al. 2009). A filter in the spatial domain exploits pixel similarities and weight kernel mask in order to generate filtered images. These filters are able to work well in homogeneous regions of an image. However in the presence of high noise, the similarity between pixels adjacent to each other gets corrupted due to which these techniques are not able to perform well. Also to preserve image edges at higher noise levels, the spatial domain filters tend to disable the denoising along edges. The processing of 2-D signals in the transform domain is based on the basic consideration of representation of the true signal with a group of basic elements. The purpose of denoising is accomplished by preserving the high magnitude coefficients and thresholding low amplitude noisy coefficients. The major transform domain techniques include BM3D, directionlet, Shearlet, and PID (Progressive Image Denoising) Dabov et al. 2007, Knaus et al. 2013). The process of convolution of the filter function with the imaging pixels make it computationally complex, and the dictionary learning methods needs thorough training  of input data sets. Therefore, for online real time applications, transform domain methods are a better selection as employ multiplication instead of convolution besides providing efficient edge preservations using multi-resolution analysis. However sometimes, even transform domain methods, fail to preserve fine feature details, and tend to blur edges.  This is because most of the techniques employ same denoising for entire range of image. Different regions of images like smooth homogenous surfaces and edges require different treatment. Hence, it is required to opt for hybrid techniques to cater to the different properties of image regions [Buades 2005, Lebrun 2012].

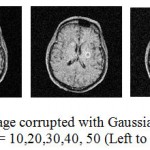Figure 1.2: Input MRI image corrupted with Gaussian Noise at standard deviation σ = 10,20,30,40, 50 (Left to Right).   Click here to View figure

The standard deviation of noise 10, 20 are considered low noise, standard deviation 30 is considered moderate noise level and standard deviation 40 and 50 are considered as high noise levels. Fig. 1.2 shows a House image contaminated with Gaussian Noise at varied levels of standard deviation.

Discussion

The varied number of significantly important denoising applications forms another major motivation for image noise suppression Goyal et al 2016, Dogra et al 2016, Ayush et al 2017, Bhawna et al 2017, Sunil et al 2018, Anchal et al 2018]. Following are major types of applications of image denoising.

Medical Image Denoising

The importance of image denoising becomes very critical when it comes to medical image denoising. The major problem with sensor image is the sensitivity to noise which can be present in a magnified form and can result in artefacts and hence can lead to increased time gap between diagnosis and treatment or even false diagnosis. Unlike commercial broadcasting of the image where the quality of the denoised image is evaluated by the extent it pleases the human eye, medical applications entail other priorities like enhancement of “features of interest” and its smoothing in any manner is intolerable.

The various types of medical modalities persistent to noise are CT (Computed Tomography), X-RAY, MRI (Magnetic Resonance Imaging), SPECT (Single Photon Emission Computed Tomography) and PET (Positron Emission Tomography. Image denoising can be considered as an area of critical importance in medical imaging as noise can be intercepted as an image deformity and it can lead to false diagnosis. So there arises an increasing requirement for denoising of the images without the image details and textures being removed [Li et al 2012].

Remote Sensing and Satellite Imaging

Remote sensing is a phenomenon in which information of an object or location is gathered without being in contact. Images acquired from remote areas and satellites finding application in weather forecasting, determines local terrains of mountains, locating natural resources like water and forests are most of the times contaminated with noise. The hyperspectral and PAN chromatic are contaminated with noise as these images are captured from a remote distance and the photographic process has to undergo atmospheric scintillations. These images have to be reconstructed to reduce noise values to put the information into practical use [Liu et al 2012].

Defense and Military Surveillance

Infrared and visible imaging is employed to for surveillance e.g., Night vision devices. These images captured to presence of atmospheric perturbations like smog and poor illumination tends the contaminate the images and thus obstructing the extraction of the important visual information. Hence these images are required to denoised in order to make them fit for further analysis [Ni et al 2008].

Industrial, Pharmaceutical and Agricultural Automation

Automated visual inspection in aerospace, textiles, food and crop industry is another important field of application of image denoising. In order to ensure the high quality of design of textile materials and metallurgical goods, they often undergo quality control measures. Therefore the images are captured in order to analyse and certify high quality of the goods. Owing the limitation of time and speedy processing of the goods, the images are often corrupted with noise. Hence these images have to denoised [Motwani et al 2004].

Conclusion

The process of removing Guassian Noise from images while preserving edges and features has long been an important research topic and is of significance importance in the field of medical imaging as the prevalence of AWGN disrupts the image quality and can often lead to false diagnosis. In other areas as well image denoising is crucial for information extraction and analysis. The variety of image denoising algorithms proposed in literature concentrate on filtering out the high frequency components which are supposedly noise values. However there are times when these components contain information of sharp edges and features are very vital to image processing tasks. Geometrical features like edges and contours play a significant role in human visual systems.  Though a large sum of directionally sensitive and sparse image transforms were devised in order to provide high degree of image representation and hence better visual quality, they still lack on the edge preservation and feature detailing aspects of the image. Hence it is important to devise image denoising algorithms which are efficient and edge preserving along with less computational complexity.

Acknowledgement

This work is supported and funded by Human Resource Development Group-Council of Scientific & Industrial Research India. All the authors of this manuscript have contributed equally in terms research findings and analysis.

References

1. Anchal.,  Goyal B., Dogra A and  Agrawal S. An Efficient Image Denoising Scheme for Higher Noise Levels using Spatial Domain Filters. Biomedical and Pharmacology Journal. 2018;11(2):625-634.
   CrossRef
2. Dogra A ., Goyal B., Agrawal S and Kamal C. A. Efficient fusion of osseous and vascular details in wavelet domain. Pattern Recognition Letters. 2017;94:189-193.
   CrossRef
3.  Goyal B.,  Ayush D and Agrawal S. Efficient representation of texture details in medical images by fusion of Ripplet and DDCT transformed images. Tropical Journal of Pharmaceutical Research.  2016;15(9):1983-1993.
   CrossRef
4. Goyal B., Dogra A and  Agrawal S. From multi-scale decomposition to non-multi-scale decomposition methods: a comprehensive survey of image fusion techniques and its applications. IEEE Access. 2017;5:16040-16067.
   CrossRef
5. Antoni B.,Coll B and Jean-Michel M. A review of image denoising algorithms, with a new one. Multiscale Modeling & Simulation. 2005;4(2):490-530.
   CrossRef
6. Antonin C. An algorithm for total variation minimization and applications. Journal of Mathematical imaging and vision. 2004;20(1-2):89-97.
7. Raymond C. H., Chung-Wa H. o and Nikolova M. Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Transactions on image processing. 2005;14(10):1479-1485.
   CrossRef
8. Dabov K., Foi A., Katkovnik V., Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Transactions on image processing. 2007 Aug;16(8):2080-95.
   CrossRef
9. Ayush D.,  Agrawal S.,  Goyal B., Khandelwal N and  Kamal C. A. Color and grey scale fusion of osseous and vascular information. Journal of computational science 2016;17:103-114.
   CrossRef
10.  Michael E and  Aharon M. Image denoising via sparse and redundant representations over learned dictionaries. IEEE Transactions on Image processing  2006;15(12):3736-3745.
    CrossRef
11.  Umesh G.,  Kumar A. S and Pandey R.  A contrast enhancement-based filter for removal of random valued impulse noise. IEEE Signal Processing Letters. 2010;17(1 ):47-50.
    CrossRef
12.  Umesh G., Kumar A. S and Pandey R.  A New Scheme for Impulse Detection in Switching Median Filters for Image Filtering. In Conference on Computational Intelligence and Multimedia Applications. 2007. International Conference on. 2007;3:442-446. IEEE.
13. Rafael G.C and Woods R. E. Image processing. Digital image processing. 2007;2.
14. Knaus C., Zwicker M. Dual-domain image denoising. In.Image Processing (ICIP), 2013 20th IEEE International Conference on. 2013 Sep;15:440-444. IEEE.
15. Darwin K . T., Alexander A. S., Timothy C.S and  Chavel P. Adaptive noise smoothing filter for images with signal-dependent noise. IEEE transactions on pattern analysis and machine intelligence. 1985;2:165-177.
16.  Marc L.,  Colom M., Buades A and Jean-Michel M. Secrets of image denoising cuisine. Acta Numerica. 2012;21:475-576.
    CrossRef
17. Shutao L .,  Yin H and Fang L.  Group-sparse representation with dictionary learning for medical image denoising and fusion. IEEE Transactions on biomedical engineering. 2012;59(12):3450-3459.
    CrossRef
18. Peng L .,  Huang F., Li G and  Liu Z. Remote-sensing image denoising using partial differential equations and auxiliary images as priors. IEEE Geoscience and Remote Sensing Letters. 2012;9(3):358-362.
    CrossRef
19. Mihcak M. K.,  Kozintsev I.,Ramchandran K and  Moulin P. Low-complexity image denoising based on statistical modeling of wavelet coefficients. IEEE Signal Processing Letters. 1999;6(12):300-303.
    CrossRef
20.  Mukesh M. C., Mukesh C. G., Rakhi C. M and Frederick C. H. Survey of image denoising techniques. In Proceedings of GSPX. 2004;27-30.
21. Pierre M and Liu J.  Analysis of multiresolution image denoising schemes using generalized Gaussian and complexity priors. IEEE Transactions on Information Theory. 1999;45(3):909-919.
    CrossRef
22.  Chao N., Li Q and Liang Z. X.  A novel method of infrared image denoising and edge enhancement. Signal Processing. 2008;88(6):1606-1614.
    CrossRef
23.  Ajit R, Rangarajan A and  Banerjee A. Image denoising using the higher order singular value decomposition. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2012;1-1.
24.  Ling S.,  Yan R.,  Li X and  Liu Y.  From heuristic optimization to dictionary learning: A review and comprehensive comparison of image denoising algorithms. IEEE Transactions on Cybernetics. 2014;44(7):1001-1013.
    CrossRef
25.  Agrawal S., Dogra A and Goyal  B. Osseous and digital subtraction angiography image fusion via various enhancement schemes and Laplacian pyramid transformations. Future Generation Computer Systems. 2018;82:149-157.
    CrossRef
26.  Rohit V and Ali J.  A comparative study of various types of image noise and efficient noise removal techniques. International Journal of advanced research in computer science and software engineering. 2013;3:10.
27. Yu H., Zhao L., Wang H. Image denoising using trivariate shrinkage filter in the wavelet domain and joint bilateral filter in the spatial domain. IEEE Transactions on Image Processing. 2009 Oct;18(10):2364-9.
    CrossRef
28.  Andrew W. B., Gloria Y. Y., Joshua A. S and  Villasenor J. Visibility of wavelet quantization noise. IEEE Transactions on image processing. 1997;6(8):1164-1175.
    CrossRef
29.  Hongtu Z.,  Li Y., Joseph G. I., Shi X ., An H., Chen Y .,  Gao W., Lin W., Daniel B. R and Bradley S. P. Regression models for identifying noise sources in magnetic resonance images. Journal of the American Statistical Association. 2009;104(486):623-637.
    CrossRef