Volume 12, number 2
 Views: (Visited 176 times, 1 visits today)    PDF Downloads: 1459

Sivasubramanian S, Namasivayam S. K. R. Optimization of Medium Components for Phenol Degradation by EM-1. Biosci Biotech Res Asia 2015;12(2)
Manuscript received on : 
Manuscript accepted on : 
Published online on:  21-12-2015
How to Cite    |   Publication History    |   PlumX Article Matrix

Optimization of Medium Components for Phenol Degradation by EM-1

S. Sivasubramanian*1, S. Karthick Raja Namasivayam2

1Department of Chemical Engineering, Faculty of Bio and Chemical Engineering, Sathyabama University, Chennai, Tamilnadu, India. 2Department of Biotechnology, Faculty of Bio and Chemical Engineering, Sathyabama University, Chennai, Tamilnadu, India.  

ABSTRACT: In this work phenol degradation was carried out using Effective Microorganism-1(EM-1) under optimized medium condition. The optimization of medium components was carried out by Plackett–Burman Design (PBD) and Central Composite Design (CCD).Screening of medium component by PB showed that initial phenol concentration(p=0.002), FeCl3(p= 0.002), MnSO4 H2O(p=0.001), MgSO4.7H2O (p=0.009) and KH2PO4   (p=0.004) had a significant effect on phenol degradation. The optimum of 96.8 % phenol degradation was observed at initial phenol concentration 1000 mg/l, FeCl3-1.5 mg/l, MnSO4 H2O-100mg/l,MgSO4.7H2O-100mg/ land KH2PO4-250mg/l.Second order polynomial regression analysis was carried out to study the interaction effects of medium composition. The R2==.9819 AdjR2= 0.99 and Pre R2= 0.981 suggested that experimental values are in good agreement with predicted values.

KEYWORDS: RSM; Plackett–Burman Design; Central Composite Design; Phenol degradation; Medium optimization

Download this article as: 
Copy the following to cite this article:

Sivasubramanian S, Namasivayam S. K. R. Optimization of Medium Components for Phenol Degradation by EM-1. Biosci Biotech Res Asia 2015;12(2)

Introduction

Phenol and phenolic compounds are hazardous pollutants from petrochemical plants, oil refineries, coking plants, pharmaceutical and dye manufacturing industries (Swoboda and Colberg, 1995).Due to  toxic property towards aquatic life and plant (Jiang et al., 2002) U.S. Environmental Protection Agency has included them in its list of priority pollutants (Neumann et al., 2004).The World Health Organization (WHO) has also set a limit level of 1 mg/l to regulate the phenol concentration in drinking waters (Yang et al.,1975 and Hannaford et al.,1999).Several methods are available for the treatment of phenolic wastewaters from these industries. The commonly used methods are adsorption, chemical oxidation and bioremediation (Annadurai et al., 2000). Bioremediation is proved to be economical and versatile approach as it leads to complete mineralization of phenol into H2O and CO2.

Various phenol-degrading microorganisms including bacteria, yeast and fungi have been studied for their ability to degrade phenol (Semple et al., 1996 and Van Schie et al., 2000).The consortium have an advantage over pure culture since it has higher degradation rate and efficiency (Sivasubramanian et al., 2014).In 1970’s Effective Micro organism (EM) was used in treatment of pollutant in Okinawa, Japan (Karthick Raja Namsivayam et al., 2011). The EM solution contains naturally occurring microbes that have the ability of reducing the biological toxicity of waste water (Higa, 1996). The different species of EM have their own respective functions. EM can be applied to many environments to break down organic matter (Zakaria et al., 2010). In this study EM-1 commercially purchased from Japan is used for phenol degradation.

RSM is an important statistical technique employed in the optimization of process parameter and media composition in biochemical industries. RSM can identify interaction effects among process parameter and it has been extensively applied for optimization of physical parameter and medium composition (Sivasubramanian et al., 2014) .In this study batch experiments was carried out to evaluate phenol degradation efficacy of EM-1.

Materials and Method

Chemicals and Reagents

Chemicals and reagents used in the study were of analytical grade. Inorganic salts used in preparing microbial growth media were of reagent grade purchased from Sigma Aldrich. Phenol was purchased from Merck, Mumbai, India. All the other chemicals used in this study were purchased from Merck, India.

Effective Microorganisms (EM-1)

Laboratory stock culture of EM-1 originally obtained from Japan contained a mixture of Lactobacillus plantarum (1.0×104 CFU/ml), Candida utilis (1.0×105 CFU/ml), Actinomycetes (3.5×103 CFU/ml), Streptomyces albus (3.0×103 CFU/ml) and Aspergillus oryzae (1.1×105 CFU/ml). EM-1 solution is a yellowish liquid with a pleasant odour, sweet taste and stored in cool place without refrigeration at 25oC.

Activation of EM-1

The activation of EM-1 was carried out as per procedure given by Sivasubramanian et al., (2014). EM-1was available in a dormant state and required activation before application. The activation involved addition of 20 liters of distilled water and 2 kg of Jaggery (pure cane sugar) to 1 liter of dormant EM-1. The mixture was poured into a clean airtight plastic container under anaerobic condition. The container was kept in dark place at ambient temperature for 8-10 days. The gas was released at regular intervals until the fermentation was complete.

Phenol Estimation

Phenol concentration was determined quantitatively by a colorimetric method, using 4-aminoantipyrine as colouring reagent. These analyses were performed according to the procedures described in Standard Method for the Estimation of Water and Wastewater (Greenberg et al., 1992).

Optimization of Medium Components

The ability of microorganisms to degrade pollutants is strongly influenced by nutritional parameters such as carbon and nitrogen sources. Therefore, it is necessary to design an appropriate media composition for maximizing the removal efficiency of phenol by EM-1. RSM is generally used to investigate a combined effect of several variables and to determine optimum conditions for a multivariable system (Montgomery, 2001).

PSD is an efficient way to identify the important factors among a large number of variables (Stanbury, 1986) was used in the present study to screen the important variables that significantly influence phenol degradation. In this study, a 12-run PSD is applied to screen the minimal media composition.

The CCD is a method that can efficiently be applied to develop the second-order response model with a few numbers of factors (Lu et al., 2009).In this work the optimization of screened variables are carried out by using CCD. A second order polynomial quadratic equation was used to predict the optimum value and subsequently to elucidate the interaction between the variables. The quadratic equation model for predicting the optimal point is expressed according to equation (1)

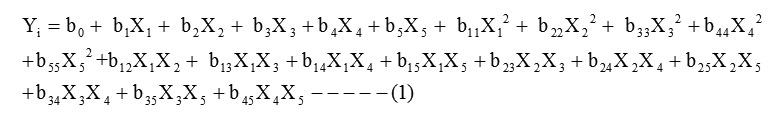
formula1

 

where Yi is the predicted response, X1, X2, X3,X4, X5 are independent variables,b0 is the offset term, b1, b2, b3,b4, b5 are  coefficient of linear effects, b11, b22, b33,b44,b55 are coefficient of squared effects and b12, b13, b14,b15,b23,b24,b25,b34,b35,b45 are coefficient of interaction terms. The regression equation contain five linear term (X1, X2, X3, X4, X5), five quadratic term (X12, X22, X32, X42, X52) and ten cross-interactions (X1X2, X1X3, X1X4, X1X5, X2X3, X2X4, X2X5X3X4, X3X5, X4X5) terms plus 1 block term. The empirical mathematical model was tested with the ANOVA with 5% level of significance. The ANOVA was used for checking the significance of the second-order models. The statistical significance of the second-order model equation is determined by F-value. In general, the calculated F-value should be greater than the tabulated F-value to reject the null hypothesis, where all the regression coefficients are zero.

Degradation Experiments

All the degradation experiment for the evaluation of phenol degrading ability was carried out in 500 ml Erlenmeyer flask containing 100 ml of MSM. For optimization of medium components for phenol degradation experiments were carried out as per composition given in design Table 2 and 5. Initial screening of medium components was done using PBD. Then the screened medium composition was optimized by CCD for phenol degradation.

Result and Discussion

Morphology of EM-1

Figure 1 shows the SEM image of EM-1 which mixture consist of Lactobacillus plantarum (1.0×104 CFU/ml), Candida utilis (1.0×105 CFU/ml), Actinomycetes (3.5×103 CFU/ml), Streptomyces albus (3.0×103 CFU/ml) and Aspergillus oryzae (1.1×105 CFU/ml).Cells of different shapes from small rods to large rods of Lactobacillus plantarum and lengthy filamentous cells of Actinomycetes. A cell of Aspergillus oryzae was visible with mycelia spore bearing structure. Candida utilis of smooth spherical shapes were also visible in the SEM image.

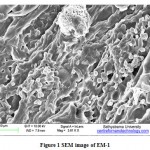Figure 1 SEM image of EM-1 Figure 1: SEM image of EM-1

Click here to View figure

 

Screening of significant variables by PB method

The medium component for phenol degradation at high level and low level is as shown in the Table 1.The matrix developed by the PB design and the resulting percentage degradation from each trial were presented in Table 2. The regression analysis and t-value of the variables by PBD are shown in Table 3.

Table 1: High and Low level of medium composition used in PB

No Variables Low
(mg/L)		 High
(mg/L)
X1 Initial Phenol concentration 750 1250
A (NH4)2SO4 200 250
B CaCl2 7 8
C FeCl3 1 2
D MnSO4H2O 50 150
E MgSO47H2O 50 150
F K2HPO4 400 600
G KH2PO4 200 300

 

Table 2: PB design for eight variables with coded values along with the predicted and observed results for phenol degradation byEM-I

Runs X1 A B C D E F G Percentage degradation Predicted

Degradation

 Residue
1 1250 200 8 1 50 50 600 300 84 83.89 0.11
2 1250 250 7 2 150 50 600 200 82.6 82.61 -0.01
3 750 250 8 2 50 150 600 200 81.5 81.51 -0.01
4 1250 250 7 2 50 50 400 300 82 81.99 0.01
5 750 200 7 2 150 150 400 300 83.2 83.09 0.11
6 750 200 7 1 50 50 400 200 81.5 81.63 -0.13
7 1250 200 7 1 150 150 600 200 84.5 84.49 0.01
8 750 200 8 2 150 50 600 300 83 83.11 -0.11
9 750 250 8 1 150 50 400 200 83 82.88 0.12
10 1250 200 8 2 50 150 400 200 82.5 82.49 0.01
11 1250 250 8 1 150 150 400 300 85 85.13 -0.13
12 750 250 7 1 50 150 600 300 82.9 82.89 0.01

 

Table 3: Regression analysis of the PB design for phenol degradation byEM-I

Predictor Coefficient SE Coefficient T P VIF
Constant 76.9167 0.9454 81.36 0 1
Phenol 0.0018333 0.0001915 9.57 0.002 1
(NH4)2 SO4 -0.005667 0.001915 -2.96 0.06 1
CaCl2 0.38333 0.09574 4 0.058 1
FeCl3 -1.01667 0.09574 -10.62 0.002 1
MnSO4 H2O 0.0115 0.0009574 12.01 0.001 1
MgSO4 7H2O 0.0058333 0.0009574 6.09 0.009 1
K2HPO4 0.0010833 0.0004787 2.26 0.109 1
KH2PO4 0.0075 0.0009574 7.83 0.004 1
R2 = 99.4% adj R2= 97.7% PredictedR2– 90%

 

Initial phenol concentration (X1), CaCl2 (B), MnSO4H2O (D), MgSO4.7H2O (E), K2HPO4 (F) and KH2PO4 (G) had positive effect on phenol degradation. Whereas (NH4)2 SO4 (A) and FeCl3 (C) had the negative effect on the percentage degradation of phenol. The variables that had a significant effect (confidence levels >95%, P < 0.05) on phenol degradation were initial phenol concentration (p=0.002), FeCl3 (p=0.002), MnSO4.H2O (p=0.001), MgSO4.7H2O (p=0.009) and KH2PO4 (p=0.004).The other variables CaCl2 (p=0.058), (NH4)2SO4 (p=0.06) and K2HPO4 (p=0.109) with p >0.05 did not affect the percentage of degradation. The regression analysis of the PBD is as shown in the equation (2)

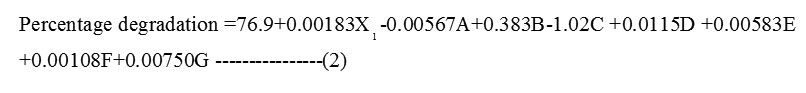
formula2

 

So the further optimization of initial phenol concentration, FeCl3, MnSO4H2O, MgSO47H2O and KH2PO4 was carried out using CCD.

Optimization of medium components by CCD

CCD was employed to determine the optimal concentration of medium components and to study the interactions effect between the significant factors that affects the percentage phenol degradation. The five independent variables were studied at three different levels as shown in Table 4.

Table 4: Coded levels for medium composition used in CCD for phenol degradation by EM-1

Variables (mg/L) Coded levels
-1 0 1
X1:Initial phenol concentration 750 1000 1250
C:FeCl3 1 1.5 2
D:MnSO4H2O 50 100 150
E:MgSO47H2O 50 100 150
G:KH2PO4 200 250 300

 

Regression analysis

A set of 50 experimental runs was carried out for 5 screened variables. The theoretical predicted values and the experimental results are represented in Table 5. Multiple regression analysis was used to analyse the data and thus a second-order polynomial equation (3) was derived from coded values

Table 5: CCD showing observed and predicted response values of phenol degradation

S.No. Initial phenol concentration

(mg/L)

 FeCl3

(mg/L)

 

 MnSO4

H2O

(mg/L)

 MgSO4 7H2O (mg/L) KH2PO4

(mg/L)

 

 Percentage degradation

Experimental

 Percentage degradation

Experimental

 Residue
1 1250 1 150 50 300 89.4 89.24 0.16
2 750 1 150 150 300 92.3 92.24 0.06
3 1000 1.5 100 100 250 95.8 95.51 0.29
4 750 2 50 50 200 91 91.11 -0.11
5 1000 1.5 100 100 324.7674 97 97.13 -0.13
6 750 2 50 50 300 91.2 91.09 0.11
7 1250 2 50 150 300 91 90.99 0.01
8 1250 2 150 150 200 90 90.3 -0.3
9 1000 1.5 100 100 175.2326 96.8 96.46 0.34
10 1000 1.5 174.7674 100 250 91 91.08 -0.08
11 750 1 50 150 300 91 90.97 0.03
12 1000 1.5 100 100 250 96 95.51 0.49
13 1000 1.5 100 25.23256 250 91.9 91.87 0.03
14 750 2 150 50 300 90 90.15 -0.15
15 1000 1.5 25.23256 100 250 91.3 91.02 0.28
16 1000 1.5 100 100 250 95.1 95.51 -0.41
17 1250 2 150 50 300 89.8 89.89 -0.09
18 1250 1 50 150 300 90 89.98 0.02
19 1250 2 150 50 200 90 89.93 0.07
20 750 2 50 150 300 91 91.4 -0.4
21 1250 2 50 50 200 91 91.12 -0.12
22 750 1 150 50 300 90 90.07 -0.07
23 1000 1.5 100 100 250 95.6 95.51 0.09
24 1000 1.5 100 100 250 95.7 95.51 0.19
25 1250 1 50 150 200 89.2 89.05 0.15
26 750 2 150 150 300 92 91.72 0.28
27 1000 1.5 100 100 250 95.2 95.51 -0.31
28 1250 1 50 50 200 89.1 89.34 -0.24
29 1250 1 150 150 300 91 90.97 0.03
30 1373.837 1.5 100 100 250 91.3 91.13 0.17
31 1000 1.5 100 100 250 95.1 95.51 -0.41
32 1000 2.24767 100 100 250 95 94.87 0.13
33 626.1628 1.5 100 100 250 92.1 92.06 0.04
34 750 1 50 50 300 90.3 90.06 0.24
35 750 1 150 150 200 91 91.33 -0.33
36 750 1 50 150 200 90 90.04 -0.04
37 1250 1 50 50 300 89.1 89.49 -0.39
38 750 2 50 150 200 90.6 90.64 -0.04
39 1000 1.5 100 100 250 95 95.51 -0.51
40 1250 1 150 50 200 89.3 89.1 0.2
41 750 1 150 50 200 90 89.94 0.06
42 750 1 50 50 200 89.9 89.9 0
43 1250 1 150 150 200 90 90.07 -0.07
44 1000 1.5 100 174.7674 250 93 92.82 0.18
45 1250 2 150 150 300 91 91.03 -0.03
46 1250 2 50 50 300 91.4 91.1 0.3
47 750 2 150 50 200 90.1 90.2 -0.1
48 1000 0.75233 100 100 250 94 93.93 0.07
49 750 2 150 150 200 91.3 90.98 0.32
50 1250 2 50 150 200 90.2 90.23 -0.03

 

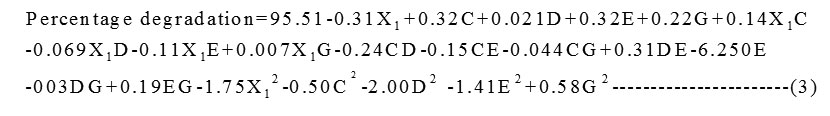
formula3

 

The coefficient of determination (R2-values) for the models are R2 =0.9940,adjustedR2=0.9900and predicted R2 = 0.9819 for the responses. The adjusted R2 and predicted R2indicate that the experimental values are in good agreement with predicted values which were observed from Figure 2.

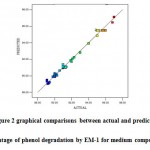Figure 2 graphical comparisons between actual and predicted percentage of phenol degradation by EM-1 for medium composition Figure 2: graphical comparisons between actual and predicted percentage of phenol degradation by EM-1 for medium composition

Click here to View figure

 

ANOVA of the response

The adequacy of the model was checked using ANOVA as shown in Table 7. The “F-value” of the model was 256.41, and the value of “Prob >F” < 0.0001, suggesting that the model was highly significant. Linear terms of X1, C, E, G and quadratic terms of X12, C2, D2, E2, G2were significant for phenol degradation. Interactive terms of X1C, X1E, CD, CE, DG, EG were also significant for phenol degradation. Whereas X1D, X1G, CG and DE are not significant with p>0.05.The model was statistically valid with a low probability value (Pmodel< 0.0001). The lack-of-fit value was not significant (P = 0.9286), indicating that the equation was adequate. The low coefficient of variation (CV =0.74%) suggested that the model was precise and reliable.

Table 6: ANOVA for the fitted quadratic polynomial model for optimization of medium composition for phenol degradation by EM-1

Source Sum of

Squares

 df Mean

Square

 F

Value

 p-value  
Prob > F  
Model 256.4143 20 12.82072 151.4182 < 0.0001 significant
X1-Phenol 3.560942 1 3.560942 42.05626 < 0.0001
C-FeCl3 3.623123 1 3.623123 42.79064 < 0.0001
D-MnSO4H2O 0.01548 1 0.01548 0.182828 0.6721
E-MgSO47H2O 3.717998 1 3.717998 43.91115 < 0.0001
G-KH2PO4 1.798494 1 1.798494 21.24099 < 0.0001
X1C 0.66125 1 0.66125 7.809647 0.0091
X1D 0.15125 1 0.15125 1.786328 0.1918
X1E 0.36125 1 0.36125 4.266518 0.0479
X1G 0.32 1 0.362 2.16230 0.9843
CD 1.805 1 1.805 21.31783 < 0.0001
CE 0.72 1 0.72 8.503509 0.0068
CG 0.06125 1 0.06125 0.723389 0.4020
DG 3.125 1 3.125 36.90759 < 0.0001
DE 0.00125 1 0.00125 0.014763 0.9041
EG 1.20125 1 1.20125 14.18728 0.0008
X12 35.8513 1 35.8513 423.4193 < 0.0001
C2 2.89979 1 2.89979 34.24776 < 0.0001
D2 46.63847 1 46.63847 550.8204 < 0.0001
E2 23.42466 1 23.42466 276.6553 < 0.0001
G2 3.879871 1 3.879871 45.82295 < 0.0001
Residual 2.455457 29 0.084671
Lack of Fit 1.436707 22 0.065305 0.44872 0.9286 Not significant
Pure Error 1.01875 7 0.145536
Cor Total 258.8698 49
 R2=.9819 AdjR2= 0.99  Pre R2= .981

 

Interaction Effect of Independent Variable

Three dimensional response surface plots graphically represent regression equations and are generally used to demonstrate relationships between the response and experimental levels of each variable. These surface plots, therefore, allow for visualization of the optimum levels of each variable for the maximum production of microbial metabolites. In a five parameter study by CCD, 3D surface plots are drawn by taking any two variables and the other three variables constant.

Figure 3.(a) shows 3D surface plot for the interaction effect between initial phenol concentration (X1) and FeCl3 (C) towards phenol degradation. The interaction between initial phenol concentration (X1) and FeCl3 (C) was significant (P =0.0091).The maximum percentage of phenol degradation 95.52% was found at 1005.03 mg/l and 1.57 mg/l of initial phenol concentration and FeCl3 (C).The percentage degradation increased when the initial phenol concentration was increased from 500 mg/l to 1000 mg/l with increase in FeCl3 (C) concentration. Then the percentage degradation decreased with increase in phenol concentration higher than1000 mg/l due to inhibitory effect of phenol at higher concentration (Ho et al. 2009)

The interaction effect between initial phenol concentration (X1) and MgSO4.7H2O (E) was also found to be significant (p=0.0479). From Figure 3. (b) it was observed that the maximum percentage of degradation was found to be 96.8% at the 950 mg/l and 107 mg/l concentration of phenol (X1) and MgSO4.7H2O (E) respectively.

Figure 3 Surface plots showing the interaction effect of (a) Initial phenol concentration (X1) and FeCl3 (b) Initial phenol concentration (X1) and MgSO4.7H2O (E) (c) FeCl3 (C) and MnSO4 H2O (D) (d) MgSO47H2O (E) and KH2PO4 (G) (e) KH2PO4 (E) and MgSO4 7H2O (D) (f) MgSO4 H2O (D) and KH2PO4 (G) Figure 3: Surface plots showing the interaction effect of (a) Initial phenol concentration  (X1) and FeCl3 (b) Initial phenol concentration (X1) and MgSO4.7H2O (E) (c) FeCl3 (C) and MnSO4 H2O (D) (d) MgSO47H2O (E) and KH2PO4 (G) (e) KH2PO4 (E) and MgSO4 7H2O (D) (f) MgSO4 H2O (D) and KH2PO4 (G)

Click here to View figure

 

The interaction effect of FeCl3 (C) and MnSO4 H2O (D) was also significant (p=0.0001). From Figure 3.(c) it was clearly observed that the maximum phenol degradation of 95.76 % was observed at concentration of 1.62 mg/l of FeCl3 (C) and112 mg/l of MnSO4 H2O(D).

The interaction effect of FeCl3 (C) and MgSO4 7H2O (E) on phenol degradation on phenol degradation was also significant (p=0.0068) as shown in Figure 3.(d). The Fe2+ ions help in the transportation materials into cells. Increase in Fe2+ ions concentration inhibits the growth of cells which in turn decreases percentage degradation of phenol. This was observed when the concentration of FeCl3 was increased from1.5mg/l to 2 mg/l.The optimum of 95.76% phenol degradation was observed at 125 mg/l and 1.56 mg/l MgSO4 7H2O(E)  and FeCl3 (C) respectively.

MnSO4.H2O (D) and KH2PO4 (G) has a significant effect (p<0.0001) on phenol degradation as shown in Figure 3.(e). Phosphate serves the construction material of cellular components such as cyclic AMP, nucleic acids, phospholipids, nucleotides and coenzymes. The optimum percentage of 96.78 % phenol degradation was found at 103 mg/l of MnSO4.H2O (D) and 276 mg/l of KH2PO4 (G). Further increase in KH2PO4 which serves as buffering agent and loss of buffering capacity leads to increase the pH of the medium which might be growth inhibiting. Therefore the percentage degradation of phenol decreases beyond 275 mg/l of KH2PO4 (G) concentration.

The interaction effect between MgSO47H2O (E) and KH2PO4 (G) was also found to be significant (p=0.0008).From Figure 3.(f) it was observed that the maximum percentage of degradation was found to be 95.76% at the 102 mg/l and 273 mg/l concentration of MgSO47H2O  (E) and KH2PO4 (G)  respectively.MgSO4.7H2O (E) and KH2PO4(G) assist initial growth of cells. In other words the interaction study showed by MgSO4.7H2O (E) and KH2PO4 (G)   was the most important component for cell growth. Once the biomass concentration increases the percentage degradation of phenol also increases. The interaction between the other independent variables such as X1D, X1G, CG and DE are insignificant since p>0.05

Validation of the Model

Validation of the statistical model was conducted by running test experiments using of initial phenol concentration 1000 mg/l, FeCl3-1.5 mg/l, MnSO4 H2O-100mg/l, MgSO4.7H2O-100mg/l and KH2PO4-250mg/l. Under these optimized conditions, the predicted response for phenol degradation was 95.7%, and the average of observed experimental values was 95.51 %. The experimental value was quite close to the predicted value, which demonstrated the validity of the model.

Conclusion

The optimization of medium components could reduce the cost required for phenol degradation in large scale. The PB and CCD was applied to assess the effect of medium composition like initial phenol concentration, (NH4)2SO4, CaCl2, FeCl3 MnSO4H2O, MgSO47H2O, K2HPO4 and KH2PO4.Based on CCD maximum of 96.8 % of phenol degradation was observed with 1000 mg/l initial phenol concentration, FeCl3-1.5 mg/l, MnSO4 H2O-100 mg/l, MgSO4 7H2O -100 mg/1, and KH2PO4– 175.23 mg/l. The determination of optimum medium condition for phenol degradation provides a platform for the use of EM-1 in environmental application for the removal of toxic organic compounds.

Reference

  1. Annadurai, G., Juang, R., Lee, D.J. Microbial degradation of phenol using mixed liquors of Pseudomonas putida and activated sludge, Waste Manage., 2002; 22:703–710.
  2. Greenberg, A.E., Clesceri, L.S., and Eaton, A.D. American Public Health Association. American Water works Association Water Environmental Federation., 1992; 207: 5.12-5.16.
  3. Hannaford, A.M., and Kuek, C. Aerobic batch degradation of phenol using immobilized Pseudomonas putida. J Ind Microbial Biotech., 1999; 22:121–126.
  4. Higa, T. Effective Microorganisms -Their role in Kyusei Nature Farming and sustainable agriculture. In Proceedings of the Third International Conference on Kyusei Nature Farming. Ed. J.F. Parr et al., USDA, Washington, USA., 1996; 20-24.
  5. Ho, K.L., Lin, B., Chen, Y.Y. Biodegradation of phenol using Corynebacterium sp. DJ1 aerobic granules, Bioresour. Technol., 2009; 100: 5051-5055.
  6. Jiang, H.L., Tay, J.H., Tay, S.T.L. Aggregation of immobilized activated sludge cells into aerobically grown microbial granules for the aerobic biodegradation of phenol, Letters in Applied Microbiology., 2002; 35: 439–445.
  7. Karthick Raja Namsivayam, S., Narendrakumar. G., Arvind Kumar, J. Evaluation of Effective Microorganism (EM) for treatment of domestic Sewage, Journal of Experimental Sciences. 2011; 2(7): 30-32.
  8. Lu, M., Yuan, D., Li.Q., Ouyang. T. Application of Response Surface Methodology to Analyze the Effects of Soil/Liquid Ratio, pH, and Incubation Time on the Bio accessibility of PAHs from Soil in In Vitro Method. Water Air Soil Pollut. 2009; 200: 387-397.
  9. Montgomery, D.C. Design and Analysis of Experiments. 5th ed., John Wiley and Sons, New York. 2001
  10. Neumann, G., Teras, R., Manson, L., Kivisaar, M., Schayer, F. Heipieper, H.J.Simultaneous degradation of atrazine and phenol by Pseudomonas sp. Strain ADP: effects of toxicity and adaptation, Applied and Environmental Microbiology., 2004; 70:1907–1912.
  11. Semple, K.T., Cain, R.B. Biodegradation of phenols by the alga Ochromonas danica. Applied and Environmental Microbiology., 1996; 62: 1265–1273.
  12. Swoboda, Colberg, N.G., Chemical contamination of the environment: sources, types, and fate of synthetic organic chemicals. In: Young, L.Y., Cerniglia, C.E. (Eds.), Microbial Transformation and Degradation of Toxic Organic Chemicals. Wiley-Liss, Inc., U.S.A., 1995; 27–74.
  13. Stanbury, P.F., Whitaker, A., Hall, S.J. Media for industrial fermentations. In: Principles of Fermentation Technology. Pergamon Press Oxford., 1986;93-122.
  14. Sivasubramanian, S., Karthick Raja Namasivayam.S. Stastical optimization of physical condition for phenol degradation using Effective Microorganism-1, Indian Journal of Chemical-Technology., 2014;21: 14-21.
  15. Van Schie, P.M., Young, L.Y. Biodegradation of phenol: mechanisms and applications, Bioremediation Journal. 2000;4: 1–18.
  16. Yang R.D.  Humphrey, A.E. Dynamic and steady state studies of phenol biodegradation in pure and mixed cultures. Biotechnol Bioeng. 1975; 17:1211–35.
  17. Zakaria, Z., Gairola, S., Shariff, N. M. “ Effective Microorganisms (EM) Technology for Water Quality Restoration and Potential for Sustainable Water Resources and Management” International Environmental Modelling and Software Society (iEMSs) International Congress on Environmental Modelling and Software Modelling for Environment’s Sake, Fifth Biennial Meeting, Ottawa, Canada,2010
(Visited 176 times, 1 visits today)

Creative Commons License
This work is licensed under a Creative Commons Attribution 4.0 International License.