Introduction

Biosignal is the term called on any signal senses from a biological tissues or medical source. These biosignals have a noise from different sources; several time- or frequency-domain digital signal processing (DSP) techniques can be used in order to remove noise also it involves: adjusting signal characteristics, spectral estimation, multiplying two signals to perform modulation or correlation, Filtering and averaging.

DSP is a technique that deals with processing signals in digital domain.ECG, EEG, EMG, ERG, EOG and others are examples of the biosignals, and all these biosignals have been tested in the frequency domain. Frequency domain give more useful information than the time domain and finding the frequency domain of the biosignal is called spectral analysis.

There are many applications of signal processing in biomedical field to perform different techniques:Echo cancellation, Noise cancellation, Spectrum Analysis, Detection, Correlation, Filters, Computer Graphics, Image Processing, Data Compression, Machine vision, Sonar, Array Processing,Guidance, robotics and etc.

This paper provides a survey on most digital signal processing techniques that used with biomedical signals to remove noises from biological signals, extract some characteristic parameter and process them.The techniques that have been introduced in this paper are[John L. et al., 2004]:Spectral Analysis, Digital Filters (FIR and IIR filters), Cross-Correlation and Coherence Analysis, Ensemble Averages, Modern Techniques of Spectral Analysis (Parametric and Non Parametric Approaches), Time–Frequency Analysis Methods like: Short Term Fourier Transform STFT (The Spectrogram), Wigner-Ville Distribution (A Special Case of Cohen’s Class, Choi-Williams and Other Distributions, Wavelet Analyses, Optimal Filter (Wiener Filters), Adaptive Filters Adaptive Noise Cancellation (ANC), Multivariate Analyses:  Principal Component Analysis (PCA) and Independent Component Analysis(ICA).

Multivariate analysis is one of the most important techniques that has wide applications in biomedical fields and can be applied for different medical signals and images. For example, this technique is commonly used with functional Magnetic Resonance Imaging (fMRI) analysis which can be applied to identify technical and physiological artifacts in fMRI.

The fMRI technique scans the whole or part of the brain repeatedly and generates a sequence of 3-D images. The voxels of the brain that represent the real activity is very difficult to be detected because of a weak signal-to-noise ratio (SNR), the presence of artifacts and nonlinear properties. Due to these difficulties and when it is difficult to predict what will occur during the acquisition of detection, using of data mining is an important as complement or as replacement of the classical methods.

Parcellation approaches use brain activity and clustering approaches to divide the brain into many parcels with some degree of homogeneous characteristics. So, the brain is divided into define regions with some degree of signal homogeneity that help for analysis and interpretation of neuroimaging data as well as mining these data because of the amount of fMRI data are huge. Independent components analysis (ICA) and Principle components analysis (PCA) algorithms are able to separate the fMRI signals into a group of the defined components, ICA regarded as the reference method to extract underlying networks from rest fMRI [Beckmann an Smith, 2004].

Second part of this paper introduces a short survey on fMRI parcellation technique and especially based on a data driven approach. Brain parcellations divide the brain’s spatial domain into a set of non-overlapping regions or modules, and these parcellations are often derived from specific data driven or clustering algorithms applied to brain images.

Biomedical Signal Processing Techniques

The techniques mentioned above are explained in details in this section as well as their utilization for data extraction from biosignals,analyzing the main characteristics and processing, finally, Table.1 which illustrates advantages, limitations and a comparison between the techniques is presented over with the conclusion.

Spectral Analysis (Classical Methods)

There are many different techniques to perform spectral analysis and each one has different strengths and weaknesses points. These methods can be divided into two categories: classical and modern methods. The first one based on the Fourier transform and the second such as those based on the estimation of model parameters. In order to determine an accurate waveform spectrum, the signal must be periodic (or of finite length) and noise loose. In many biomedical applications, the problem is that the biosignal waveform is either infinite or of adequate length, so only a part of it is available for analysis. These biosignals are often distorted with noise, and if only a part of the actual waveform can be analyzed and/or if this biosignal includes noise, here all spectral analysis techniques must be used in order to approximate and so are estimates of the correct spectrum. Most of the spectral analysis techniques try to improve the estimation accuracy of specific spectral features.

Generally, Spectral analysis method assume as the most DSP techniques that used with biosignal analysis, so it’s important to know how different phenomena effect on the spectrum of the desired signal in order to interpret it correctly.

[Marple S.L., 1987],has presented a long and rich history for developed approaches for spectral analysis decomposition. [Abboud et al., 1989], have introduced a study on interference cancellation in FECG (FetalElectrocardiograms) signal as recorded from the mother’s abdomen and calculated the spectral curves of the averaged fetal and MECG (Maternal Electrocardiograms). These power spectrums were calculated by subtraction of an averaged MECG waveform using cross-correlation function and fast Fourier transform algorithm. This technique is not effective because of the weakness in SNR, high rate of consistency between maternal and fetal ECG, and the symmetry in the frequency spectra of the signal and noise components.

The classical Fourier transforms (FT) approach is the most popular techniques used for spectral estimation.

One of the advantages of the Fourier transforms (FT) method is that the sinusoidal signals have energy at only one frequency, and if the signal is divided into a series of cosines and sines with different frequencies, but the amplitude of these sinusoidal signals must be proportional to the frequency component consisted in the signal at those frequencies.An average periodogram is the approach that used for estimating the power spectrum of the signal waveform when this power spectrum is based on using Fourier transform followed by averaging it. Welch method is one of the most important methods to find the average periodogram. This method used for estimating the power spectrum divides the data in several epochs, over lapping or non overlapping, then performs an FFT on each epochs, calculate the magnitude squared (i.e., power spectrum), then averages these spectra.

For example, in Fig.1the basic Fourier transform routine (fft) was applied EEG data,while in Fig.2 the Welch power spectral method was applied to the same array of data that was used to produce the spectrum of Fig.1.A triangular window was applied and the segment length was 150 points and segments overlapped by 50%.

Comparing the spectrum in Fig.2 with that of Fig.1 appears that the background noise is extremely reduced and became smoother.

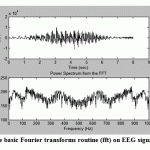Figure.1: The application of the basic Fourier transforms routine (fft) on EEG signal to produce the spectrum Click here to view full figure

 

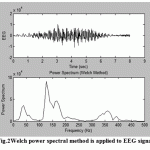Figure.2: Welch power spectral method is applied to EEG signal Click here to view full figure

Digital Filters

Most signal waveforms are narrowband with respect to noise which most of it is broadband, and white noise is regard as the broadest noise band with a flat spectrum; for this reason, filters are used. Since the aim of using filters are to reshape the spectrum in order to provide some improvement in SNR,so they are closely related to spectral analysis.Filters can be divided into two groups according to the way that they achieve the reshape of the spectrum, finite impulse response (FIR) filters and infinite impulse response (IIR) filters, and based on their approach.IIR fılters are more efficient in terms of computer time and memory than FIR filters; this is the disadvantage of FIR filters. While the advantages of FIR filter are: firstly they stable and have linear phase shifts, secondly have initial transient responses of limited length.

FIR adaptive filters was developed by [Widrow et al., 1975; 1976a]who proved that in order to obtain good performance high-order filters must be used and especially at low SNR. [Widrow et al., 1976b], they introduced study which included a comparative between three adaptive algorithms (LMS, differential steepest descent and the linear random search) and proved that there are a lot of advantages by using FIR filter like: ensured stability, simplicity and the filter rendering is not optimal.[Benjamin, 1982],has introduced study using a signal modeling approach and reporting a general form of a noise cancellation by combining two Infinite Impulse Response (IIR) filters namely a noise canceller and a line enhancer.[Fergjallah et al., 1990] have used frequency domain digital filtering techniques with application to the ECG for power-line interference removal.[Outram et al., 1995] have presented two techniques novel optimum curve fitting and digital filtering techniques to improve the feature of the FECG with minimum distortion and to measure its features like time constants, amplitudes and areas.[Stearns et al., 1996], they introduced a good treatment of the classical Fourier transform and digital filters and all basic digital filters can be interpreted as linear digital, also they covers the LMS adaptive filter algorithm. [Ingle et al., 2000], excellent treatment of classical signal processing methods including the Fourier transform and both FIR and IIR digital filters have been introduced. In 2003 a different step size LMS for possible improvements in the performance of adaptive FIR filters in non-stationary environments have introduced by [Joonwan Kim et al., 2003].

Nonrecursive is the term named FIR filters and according to Eq. [1],the inputonly (first term) is used in filter algorithm not the output:

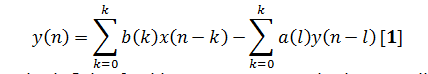
This leads to an impulse response that is finite, for this reason FIR name is given.Application and design of FIR filters using only convolution and FFT, because the impulse response of the filter process is the same as FIR coefficient function.

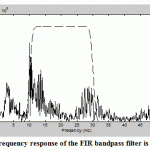Figure.3: Frequency response of the FIR bandpass filter is shown Click here to view full figure

Fig.3 shows the application and construction of FIR bandpass filter to an EEG signal using convolution and FFT to evaluate the filter’s frequency response.

Firstly and in order to show the range of the filter’s operation with respect to the frequency spectrum of the EEG data, a spectrum analysis is implemented on both the EEG data and the filter by using the FFT to analyze the data without windowing or averaging as shown in Fig.4 shows the result of applying this FIR bandpass filter to the EEG signal

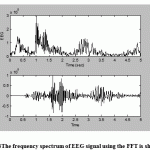Figure.4: The frequency spectrum of EEG signal using the FFT is shown Click here to view full figure

Above: Aportion of unfiltered EEG data.

Lower: The FIR bandpass filtered application to EEG signal.

Unlike FIR filters, IIR filters and according to Eq. [1] the input and output are used in filter, so the design of IIR filters is not as simple as FIR filters and most of the principles of analog filter design can be used with IIR filters. Also IIR filters can be duplicated as all the famous analog filters types (Butterworth, Chebyshev Type I and II, and elliptic).IIR filters can recognize a specific frequency norm (cutoff sharpness or slope) with lower filter order.This is the essential advantage of IIR against FIR filters. While the main disadvantage of IIR filters is that they have nonlinear phase characteristics.

Cross-Correlation and Coherence Analysis

These two techniques used with any pairs of signals(stochastic, deterministic and multichannel signal), and they are very effective in determining the relationships between pairs of biomedical signal.

In 1986 a cross correlation analysis procedure has been introduced by [Levine et al., 1986]through removing ECG signals distorted from the Diaphragmatic Electromyogram (EMGdi).

Ensemble Averages

Ensemble average deals with sets of data and especially in a random process when the probability density function is not known. These data are obtained when many records of the signal are possible; such many records could be taken from many sensors.

[Hae-Jeong Park et al., 2002],have used two-step process in the interference cancellation in EEG signal which: detection the ECG artifact by using the energy interval histogram method and ECG artifact removal by adjustment of ensemble average subtraction.

In many biosignals, the multiple records obtain from repeated responses to the same sensor in the same place.Then these sets of data are collected and added point by point. If the size of the ensemble average is equal to factor x (for example), then Signal to Noise Ratio (SNR) improves by factor .

We can conclude that the signal in ensemble averaging is not necessary to be periodicbut it must be repetitive, while the noise not correlated to the signal but must be random. As well as, the transient position of each signal must be known.

The multiple signals recorded through eye movement (shown upwardin Fig.5), and an ensemble of individual was taken.While downward, the ensemble average is founded by taking the average at each point in time for the individual responses. The extended vertical line at the same time through the upper and lower traces is the average of the individual responses at that time.

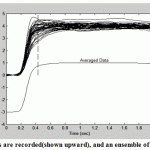Figure.5: Multiple signals are recorded(shown upward), and an ensemble of individual was taken Click here to view full figure

Modern Techniques of Spectral Analysis

These techniques are designed to overcome some distortions generated from the classical techniques, and especially when the introduced data segments are short. All the classical approaches are based on the Fourier transform, and any waveform out of the data window istacitly assumed to be zero and this assumption is scarcely true, so such a proposition can produce distortion in the estimate as well as the distortions caused by diverse data windows (including the rectangular window).Modern approaches divided into two wide classes: parametric (model-based) and nonparametric(eigen decomposition).

[Marple S.L., 1987], introduced rigorous treatment of Fourier transform, parametric modeling methods (including AR and ARMA), and eigen analysis-based techniques.[Shiavi R., 1999], emphasizes spectral analysis of signals buried in noise with excellent coverage of Fourier analysis, and autoregressive methods have been presented, as well as good introduction to statistical signal processing concepts.

Parametric Approach

The need for windowing in the classical techniques will be removed by using parametric approach, and it can improve spectral resolution and fidelity especially when the waveform includess a large amount of noise, but itprovides only magnitude acquaintance in the form of the power spectrum as well as needs more decision in their application than classical methods.

Generally, a linear process is referred to as a model in parametric method to estimate the power spectrum, and this model is simulated to be driven by white noise.The output of this model is compared with the input so that the model parameters set for the best match between output and the waveform of interest in order to give the best assessment of the waveform’s spectrum.

In this approach there are various model types are used and differentiated according to their transfer functions, the most three common models types are:autoregressive (AR), moving average (MA), and autoregressive moving average (ARMA). The selection of which one is the most convenient model than other, requires some learning of the probable shape of the spectrum waveform. For example, the AR model is especially used for evaluating sharp peaks spectra but no deep hollows, so it’s transfer function has a constant in the numerator and a polynomial in the denominator and is sometimes called an all-pole model as same as an IIR filter with a constant numerator.Inversly the MAmodel is useful for estimating spectra with the hollows but no sharp peaks, so it’s transfer function has only a numerator polynomial and is called an all-zero model and is similar to an FIR filter.ARMA model is combines both the AR and MA features and used with the spectrum that contain both sharp peaks and the hollows; so it’s transfer function has both numerator and denominator polynomials and is called a pole–zero model.

Weakness in the MA model that restricts its advantage in power spectral estimation of biosignals is unability to model narrowband spectra well. Thus only the AR model is used in power spectral analysis.Accorsing to algorithms that process data,AR spectral estimation techniques can be divided into two classes: process block data (when the entire spectrum waveform is available in memory) and process data sequentially (when incoming data must be estimated rapidly for real-time considerations).only block processing algorithms will be considered in this research as they locate the major application in biomedical engineering and are the only algorithms processed in the MATLAB Signal Processing Toolbox. There are many approaches for estimating power spectrum and the AR model coefficients directly from the waveform. There are four approaches which have received the most interest are: the Yule-Walker, the Burg, the covariance and the modified covariance methods.

Non Parametric Approach

For obtaining better frequency estimation characteristics and better resolution especially at high noise levels, Eigen analysis(frequency estimation) spectral methods are the promoted one; so they can remove much of the noise contribution and especially effective in recognize sinusoidal, exponential, or other narrowband processes in white noise. When the noise is colored (i.e. not white but contains some spectral features), there doing can be decadent; as well as are not well-suited to estimating spectra that contain broader-bandfeatures.

The main characteristic of eigenvector approaches is to divide the information comprised in the data waveform or autocorrelation function into two subspaces: a signal subspace and a noise subspace.The Eigen decomposition output eigenvalues with decreasing order and orthonormal eigenvectors, and if those eigenvectors that are considered portion of the noise subspace are removed, the effect of that noise is functionally cancelled. Functions can be counted based on either signal or noise subspace and can be sketched in the frequency domain displaying sharp peaks where sinusoids or narrowband processes exist. So the main problem of applying eigenvector spectral analysis is the selection of a suitable dimension of the signal (or noise) subspace.

Generally, parametric methods are more complicated than the nonparametric but the later techniques are not deemed correct power spectral estimators because the nonparametric approach do not keep signal power and cannot be able to reconstruct the autocorrelation sequence by applying the Fourier transform to estimators.So the best termed for this approach is frequency estimator because it extend spectra in relative units.In MATLAB there are two popular versions of frequency estimation based on eigenanalysis available in the Signal Processing Toolbox. These eigenvector spectral analysis methods are the MUltiple SIgnal Classifications (MUSIC) and the Pisarenko harmonic decomposition (PHP) algorithms.

Fig.6 shows spectrum obtained using 3 different methods applied to an EEG data waveform, and comparison between classical FFT-based (Welch method) without window nor overlap, autoregressive (Modified Covariance Spectrum) and eigenanalysis without window nor overlap (MUSIC Method) spectral analysis methods; (e) plot the singular values from the eigenvector routine as determined by pmusic with high subspace dimension to get many singular values.

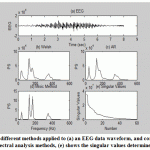Figure.6: Shows spectrum obtained from 3 different methods applied to (a) an EEG data waveform, and comparison between (b) classical, (c) AR and (d) eigenanalysis spectral analysis methods, (e) shows the singular values determined from the eigenvalues. Click here to view full figure

From this figure we conclude that the most strength and clearly identifies components is the eigenvector method (d); while the spectrum created by the classical Welch method does detect the peaks but also shows a number of other peaks in response to the noise, so it would be complicated to locate and definitively the signal peaks from this spectrum. Also the AR method detects the peaks and so smooth’s the noise, but such the Welch spectrum it shows pseudo peaks concerning the noise, so it also would be complicated to exactly locate the frequencies of the peaks from this spectrum. While the eigenanalysis spectral analysis methods fix the peaks frequencies with an excellent frequency resolution. Plot (e) in this figure shows the singular values determined from the eigen values that can be used to estimate the dimensionality of multivariate data, i.e. produce a curve in order to examine a break point(or change in slope) between a sharp and smooth slope, then this break point is possessed as the dimensionality of the signal subspace. The concept is that a soft decrease in the singular values is associated with the signal noise while a faster indicates that the singular values are associated with the signal. Regrettably, well definition in break points is not always located when real data are involved.

Time–Frequency Analysis

The main concern in many biomedical signals and medical images is on timing information because many of these waveforms are not stationary. For example, the EEG signals variation extremely relying on different inner cases of the object like:eyes closed,meditation or sleep.While classical or modern spectral analysis methods provide a good and complete processing for waveforms that are stationary, many approaches have been advanced to extract both frequency and time information from a waveform (Fourier transformenable to describe both time and frequency characteristics of the waveform). Essentially these approachescan be divided into two groups: time–frequency methods and time–scale methods(Wavelet analyses).[Boashash B., 1992], in early chapters he provided a very useful introduction to time–frequency analysis followed by a number of medical applications.

Fourier transform provides a good representation of the frequencies in a waveform but not their timing, while in the phase portion of the transform the timing is encoded but this encoding is hard to explain and progress.

Short-Term Fourier Transf. (The Spectrogram)

This is the first straightforward approach has been advanced to extract both frequency and time information from a waveform which based on slicing the waveform into a digit of short segments, and by using the standard Fourier transform the analysis on each of these segments is done. Before the Fourier transform is applied to that segment, a window function is applied to a segment of data in order to isolate it from the waveform. Since the Fourier Transform is applied to a segment of data that is shorter than the overall waveform then is termed STFT(short-term Fourier transform)or the spectrogram. The spectrogram has two main troubles (1) An optimal window length selection for data segments which have various features may not be possible and (2) The time–frequency trade off, i.e. when the data length is shorten to improve time resolution (made smaller window) then it will reduce frequency resolution and vice versa, beside it could also effect on the waste of low frequencies that are no longer fully included in the data segment. This trade off has been equated so the product of time and frequency resolution must be bigger than some minimum.

Despite these restrictions, spectrogram or STFT has been used successfully in a wide variety cases and especially in a number of biomedical applications where only high frequency components are of interest and frequency resolution is not critical.

The spectrogram can be generated in MATLAB either by using the standard fft function or by using a special function of the Signal Processing Toolbox.

Wigner-Ville Distribution (A Special Case of Cohen’s Class)

The trade-off between time and frequency resolution in the spectrogram or STFT and to overcome some of these shortcomings, a number of other time–frequency methods has been developed and the first of these was the Wigner-Ville distribution. This dual nameis due to its development which was used in physics by Wigner, and then used in signal processing by Ville.Itis deemed as a special case of similar wide variety transformations of Cohen’sclass of distributions. [Boashash et al., 1987], they proposed practical information on calculating the Wigner-Ville distribution.[Cohen L., 1989], he introduced classic review article on the various time-frequency methods in Cohen’s class of time–frequency distributions

The Wigner-Ville distribution and all of Cohen’s class of distributions; use autocorrelation function for calculating the power spectrum approach by using a variation of the autocorrelation function where time remains in the result and unlike the standard autocorrelation function where time is summed or integrated out of the result which is only a function of the shift or lag.As in the classic approach for computing the power spectrum was to take the Fourier transform of the standard autocorrelation function and in order to construct this autocorrelation function, the waveform is compared with itself for all possible relative lags or shifts.

For using with these distributions, an equation is introduced here in both continuous and discreet formEq. [2, 3]:

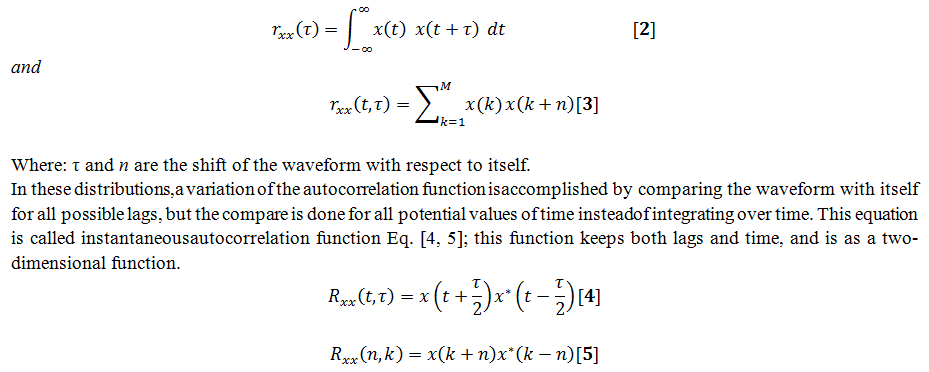
Where: τ and n are the time lags as in autocorrelation, and * represents the complex conjugate of the signalx.

Actually most actual signals are real, soEq. [3] can be applied to either the real signal itself or a complex part of the signal which is known as the analytic signal.

This distribution has a number of advantages and shortcomings against STFT,it greatest strength is that produces definite or good picture of the time–frequency structure. The Wigner-Ville distribution has many characteristics the same as of the STFT while only one property not participated by the STFT which is finite support in time (the distribution is zero before the signal starts and after it ends) and frequency (the distribution does not contain frequencies beyond the range of the input signal).Because of the cross products, this distribution is not necessarily zero whenever the signal is zero and this Cohen’s property called strong finite support.

While the most serious shortcoming is the production of cross products which will produce time–frequency energies that are not exist in the original signal, although these are contained within the time and frequency boundaries of the original signal.This property has been the main impulse for the improvement of other distributions that introduce different filters to the instantaneous autocorrelation function to qualify the damage caused by the cross products.

As well as, the Wigner-Ville distribution can have negative regions with no meaning; also it has week noise properties, because cross products of the noise and essentially when the noise is distributed across all time and frequency. In some cases, a window can be used in order to reduce the cross products and noise influences, andthe desired window function is applied to the lag dimension of the instantaneous autocorrelation function. So windowing is a compromise sought between a reduction of cross products and loss of frequency resolution.

The Choi-Williams and Other Distributions

The general equation for determining a time–frequency distribution from Cohen’s class of distributions is defined by Eq. [6];this equation is rather formidable but can be simplified in practice:

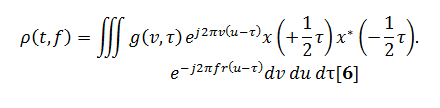
Where:g(v,τ) is known as a kerneland provides the two-dimensional filtering of the instantaneous autocorrelation.

These other distributions are defined by Eq. [6] and now the kernelg(v,τ) is no longer 1. Eq. [6] can be simplified two different forms:

• The integration with respect to the variable v can be performed in advance since the rest of the transform (i.e., the signal portion) is not a function of v; for any given kernel.
• Or use can be made of an intermediate function, called the ambiguity function.

One popular distribution is the Choi-Williams (exponential distribution ED) because it has anexponential-type kernel. It is having reduced cross products as well as has better noise characteristics than the Wigner-Ville.

[Boudreaux et al., 1995], they presented an exhaustive, or very nearly so, compilation of Cohen’s class of time-frequency distributions.

Analytic Signal

Analytic Signal is a modified version of the waveform and all transformations in Cohen’s class of distributions produce better results when applied to it. When the real signal can be used, the analytic signal (a complex version of the real signal) has several advantages. One of the most important advantages is that the analytic signal does not contain negative frequencies, so its use will reduce the number of cross products. Also the sampling rate can be reduced when the analytic signal is used. The analytic signal can be constructed by using several approaches.

Now the different members of Cohen’s class of distributions can be implemented by a general routine that starts with the instantaneous autocorrelation function, evaluates the appropriate determining function, filters the instantaneous autocorrelation function by the determining function using convolution, then takes the Fourier transform of the result. In this paper the routine is set up to evaluate EEG signal treated with four various distributions: Wigner-Ville distribution (as the default), Choi-Williams, Born-Jorden-Cohen and Rihaczek-Margenau,

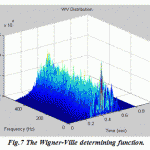Figure.7: The Wigner-Ville determining function Click here to view full figure

 

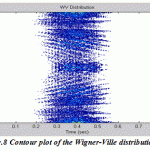Figure.8: Contour plot of the Wigner-Ville distribution Click here to view full figure

 

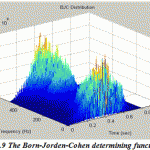Figure.9: The Born-Jorden-Cohen determining function Click here to view full figure

 

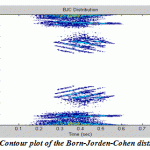Figure.10: Contour plot of the Born-Jorden-Cohen distribution Click here to view full figure

 

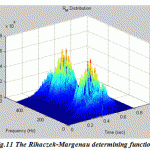Figure.11: The Rihaczek-Margenau determining function Click here to view full figure

 

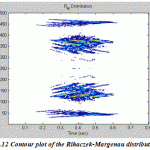Figure.12: Contour plot of the Rihaczek-Margenau distribution Click here to view full figure

 

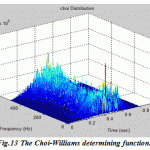Figure.13: The Choi-Williams determining function Click here to view full figure

 

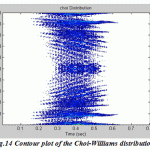Figure.14: Contour plot of the Choi-Williams distribution Click here to view full figure

Wavelet Analysis

Wavelet transform used as another method to describe the properties or processing biomedical images and a non stationary biosignal waveform (that change over time). The wavelet transform is divided into segments of scale rather than sections of time, and it is applied on a set of orthogonal basis functions obtained by contractions, dilations and shifts of a prototype wavelet.

The main difference between wavelet transforms and Fourier transform-based methods is that the Fourier transform-based methods use windows of constant width while the wavelet uses windows that are frequency dependent.

By using narrow windows for high-frequency components,wavelet transforms enable arbitrarily good time resolution whereas the wavelet transforms enable arbitrarily good frequency resolution by using broad windows for low-frequency components.The continuous wavelet transform (CWT) can be represented mathematically in Eq. [7]:

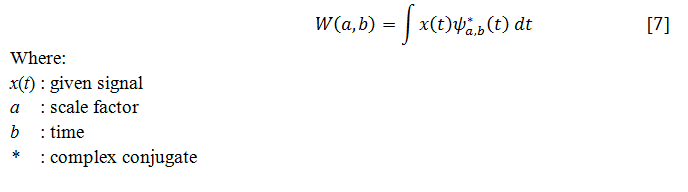
Probing function is called “wavelet” because it can be any of a number of different functions so it always takes on an oscillatory form.Also a prototype wavelet function is termed a mother wavelet when b = 0 and a = 1, then the wavelet is in its natural form, that is, .

The orthogonal basis functions denoted by  are obtained by scaling and shifting by scale a and time b respectively Eq. [8]:

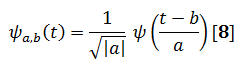
By adjusting the scale factor, the window duration can be arbitrarily changed for different frequencies, i.e.if a is greater than one then the wavelet function is stretched along the time axis where as when it is less than one (but still positive) it contacts the function. Negative values of a simply flip the probing function on the time axis.

Because of the redundancy in the transform by using CWT coefficients then it is rarely performed recovery of the original waveform using CWT coefficients, while the more parsimonious discrete wavelet transform DWT when reconstruction of the original waveform is desired.The redundancy in CWT is not a problem in analysis applications but will be costly when the application needs to recover the original signal because for recovery, all of the coefficients (that are generated due to oversampling many more coefficients than are really required to uniquely specify the signal) will be required and the computational effort could be too much.

While the DWT may still require redundancy to produce a bilateral transform except if the wavelet is carefully chosen such that it leads to an orthogonal family or basis in order to produce a non redundant bilateral transform.

[Wickerhauser, 1994], rigorous and extensive treatment of wavelet analysis was presented.

[Aldroubi et al., 1996], they presented a variety of applications of wavelet analysis to biomedical engineering.In 1996 a new wavelet analysis method was implemented by [Ye Datian et al, 1996] in the detection of FECG from abdominal signal, while [Echeverria et al., 1996]have used wavelet multi resolution decomposition and a pattern matching procedure in the same year, but the output result still combined the MECG. [Rao et al., 1998], good development of wavelet analysis was presented including both the continuous and discreet wavelet transforms.Also in the same year, a new method called Wavelet Analysis and Pattern Matching (WA-PM) was developed by [Echeverria et al., 1998].

This procedure was used for processing the abdominal ECG in the off-line, so the disadvantage of this method is time consuming, while the authors have proved that it is a reliable procedure for the additive noise reduction and maternal QRS cancellation.

[Conforto et al., 1999],they found that the wavelet filter gives excellent implementation in input conservation and time-detection of EMG impulses distorted with artifacts when made comparison between four techniques deals with motion artifact removal from EMG signal: 8^th order Chebyshev HPF, moving average filter (MA), moving median filter and finally using an adaptive filter based on orthogonal Meyer wavelets. In 2000 a wavelet transform based method was developed by [Khamene et al., 2000]to extract the FECG from the combined abdominal signal.

[Mochimaru et al., 2002], they have used wavelet theory to detect the FECG, and he concluded that this method gives good time resolution and weak frequency resolution at high frequencies, and good frequency resolution and weak time resolution at low frequencies. Also in this year, a wavelet based denoising technique has been proposed by [Tatjana Zikov et al., 2002] for ocular artifacts removal in EEG signal. This method is unsupported on the reference EOG or visual performance. While in the same year, statistical wavelet threshold have been used by [Browne et al., 2002],which is capable of recognizing the EEG and the artifact signals and separating localized artifacts in the time-frequency domain or that have a spectrum which is uncharacteristic of the EEG.

The author concluded that this method is best when compared with specialized methods that used for artifact elimination in some cases, but it has a disadvantage that it fail to get better the elimination of baseline drift, eye movement and step artifact.

[Grujic et al., 2004], they have compared wavelet and classical digital filtering that used for denoising of Surface Electromyogram (SEMG) signals, the results show that the main advantages of wavelet technique are: the filtered signal with no artificial information inserted on it and the signal components may be separately threshold in order to generate the filtered signal. While the main disadvantage is that the definition of a mother wavelet as a priori and this selection may affect the final results. In the same year, [Azzerboni et al., 2004], they have proposed a method that used wavelet transform and ICA combination for removing the artifacts in surface EMG, according to this study, the author found that in order to identify the artifact user interface is needed. Also in the same year, [Inan Güler et al., 2004] have proposed a new approach based on Adaptive Neuro Fuzzy Inference System (ANFIS) for detection of ECG changes in patients with partial epilepsy which is implemented in two steps: feature extraction using the wavelet transforms and the ANFIS. The author concluded that the proposed ANFIS is effective in detecting the ECG changes in patients with partial epilepsy.

[Jafari et al., 2005], they have used Blind Source Separation (BSS) in the wavelet domain, so he managed the problem of FECG extraction and especially when the surrounding is noisy and time varying. In the same year, [Ping Zhou et al., 2005]have presented the performances of different methods that used for ECG artifact removal like: HPF, spike clipping, template subtracting, wavelet threshold and adaptive filtering. He examined the ECG artifacts removal from the myoelectric prosthesis control signals, taken from the reinnervated pectoralis muscles of a patient with bilateral amputations at shoulder disarticulation level.

Filter Banks

DWT-based analysis, for most signal and image processing applications, is easier to understand and implement using filter banks.

[Strang et al., 1997], they introduced thorough coverage of wavelet filter banks including extensive mathematical background.

Subband coding is using a group of filters to divide up a signal into different spectral components. Fig.15shows the basic implementation of the DWT that is the most uses as a simple filter bank which consisting of only two filters (lowpass and highpass)applied to the same waveform and also filter outputs consist of a lowpass and highpass subband.

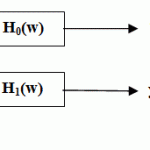Figure.15: Simple filter bank Click here to view full figure

The analysis filters is the Filter Bank that decomposes the original signal while the syntheses filters is the filter bank that reconstructs the signal. FIR filters are used throughout because they are stable and easier to implement.

Wavelet analysis is a good technique when it is used especially with signals that have long durations of low frequency components and short durations of high frequency components like EEG signals or signals of differences in inter beat (R-R) intervals.

Wavelet analysis based on filter bank decomposition is especially beneficial for detecting small discontinuities in a waveform and it is sensitive for detecting small changes even when they are in the higher derivatives. This feature is also beneficial in image processing.

Fig.16 shows the ECG signal generated by the analysis filter bank with the top-most plot showing the outputs of the first set of filters with the finest resolution, the next from the top showing the outputs of the second set of set of filters, etc. Only the lowest (i.e., smoothest) lowpass subband signal is included in the output of the filter bank; the rest are used only in the determination of highpass subbands. The lowest plots show the frequency characteristics of the high and low pass filters.

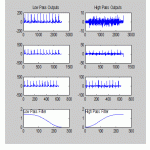Figure.16: ECG signal generated by the analysis filter bank Click here to view full figure

Advanced Signal Processing Techniques: Optimal and Adaptive Filters

The first used methods for interference cancellation were the non-adaptive interference cancellation techniques, and Wiener optimal filtering was one of the widely used non-adaptive techniques. The drawbacks of the Wiener filter are the requirements of autocorrelation matrix and cross-correlation vector which is a time consuming process because it involves matrix inversion. Due to these limitations,Adaptive Interference Cancellation (AIC) has been used to rectify wiener optimal filtering restrictions.

Optimal Signal Processing, Wiener Filters

By using FIR and IIR filters design, the user is unable to know which frequency characteristics are the best or any type of filtering will be so effective on splitting up noise from signal, so in this case the user will depend on his knowing on signal or source features or by trial and error.

For this reason an optimal filter theory was advanced to select the most suitable frequency characteristics for processing by using various approaches with a wide range depending on signal and noise properties. Wiener filter is a good developed and popular type of filters that can be used when a representation of the required signal is available.A linear process (either an FIR or IIR filter) is operated when the input waveform has signal and noise and FIR filters more popular process are used due to their stability. The basic concept of Wiener filter theory is to reduce the variation between the filtered output and some required output, this reduction is based on the least mean square approach which set the filter coefficients to minimize the square of the difference between the required and real waveform after filtering.

[Haykin, 1991], he introduced a definitive text on adaptive filters including Weiner filters and gradient based algorithms.

The Wiener-Hopf approach has other different applications like interference canceling,systems identification, and inverse modeling or deconvolution as well as standard filtering.

Adaptive Signal Processing

Unlike classical spectral analysis methods, FIR and IIR filters and Wiener filter that cannot respond to changes that might happen through the path of the signal, adaptive filters have the ability of modifying their properties according to selected properties of analyzed signal;i.e. the filter coefficients are adjusted and applied in an ongoing basis in adaptive filter while in the Wiener filter(a block approach)the analysis is applied to the complete signal and then the resultant optimal filter coefficients will applied to the complete signal.

An ideal adaptive filter paradigm is designed to make the filter’s output as close to some desired response as possible by reducing the error to a minimum through modifying the filter coefficients based on some signal property by a feedback process. The FIR filters with stability criteria make them effective in optimal filtering and adaptive applications [Ingle et al., 2000]. For this reason, the adaptive filter can be performed by a set of FIR filter coefficients.

The similarities between optimal and adaptive filter are: firstly, the nature of the desired response that depend on the given problem and its formulation which regarded as the most complex part of the adaptive system specification [Stearns et al., 1996]; secondly,the problem with an error minimization between the input and some required output response and this reduction is based on the squared error that is minimized to construct a desired signal.

LMS recursive algorithm is a simpler and more popular approach which is based on gradient optimization when it is adapted for use in an adaptive environment with the same Wiener-Hopf equations [John L. et al., 2004].The LMS algorithm uses a recursive gradient method also called the steepest-descent method for detection the filter coefficients that output the minimum sum of squared error.The advantage of the LMS algorithm is simple and easy of mathematical computation, while the drawbacks of this method are the influence of non-stationary interferences on the signal, the influence of signal component on the interference, computer word length requirements, coefficient drift, slow convergence rate and higher steady-state error.

Adaptive filter has a number of applications in biomedical signal processing. For example, it can be used to eliminatea narrowband noise 60 Hz line source that distorts a broadband signal, or inversely it can be used to eliminate broadband noise from a narrowband signal and this process is called adaptive line enhancement (ALE)or Adaptive Interference Suppression. In ALE the narrow band component is the signal while in adaptive interference suppression it is the noise.Also it can also be used for different applications same as the Wiener filter like inverse modeling, system identification and adaptive noise cancellation (ANC) which is the most important application in biomedical signal processing, this application require convenient reference source to be correlated with the noise but not the signal of interest.

[Suzuki et al., 1995], they have advanced a real-time adaptive filter for cancelling of the surrounding noise during lung sound measurements. [He et al., 2004], they have proposed a method based on adaptive filtering for cancelling ocular artifacts by recording separately two reference inputs (vertical and horizontal EOG signals) and then subtracted from the original EEG. Recursive Least Square (RLS) algorithm was used to follow the non-stationary portion of the EOG signals, the author concluded that this method is easy to implement, stable, converges fast and suitable for on-line removal of EOG artifacts.[Marque et al., 2005], they have developed an adaptive filtering algorithm particularly for removing the ECG signal distorted Surface Electromyogram (SEMG). The procedures of this study are: firstly record the ECG with a shape similar to that found in the distorted SEMGs; secondly tested the competence algorithms on 28 erector spinae SEMG recordings. The best results have been got by using the simplified formulation of a fast Recursive Least Square algorithm.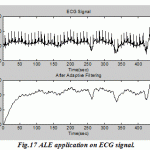

Figure.17: ALE application on ECG signal Click here to view full figure

Multivariate Analyses

Principal component analysis (PCA) and independent component analysis (ICA) sign into a section of statistics known as multivariate analysis. Due to the name “multivariate” its means that the analysis of multiple measurements or variables, but actually manages them as a single existence i.e. variables from various measurements produced on the same systemor process so these different variables are often represented as a single vector variable that has the multiple variables.

The aim of multivariate analysis is to manage transformations and reduce the dimensionality of the multivariate data set that output the data group smaller and simplest to recognize by transforming one set of variables into a new smaller.

One of the applications in biomedical signal processing is shown in EEG signal analysis where many signals are recorded from electrodes placed in the region of the cortex around the head and these multiple signals are acquired from a smaller number of neural sources and perform combinations with the EEG signals.

The two techniques PCA and ICAvary in their objectives and the standards that used to the transformation.

In PCA, the purpose is to transform the data set so into a new smallest set of variables that are uncorrelated, i.e. minimize the dimensionality of the data (not important to output more meaningful variables) by rotating the data in M-dimensional space. While in ICA the purpose is a little different by detecting new variables or components that are both statistically independent and nongaussian.

Principal Component Analysis (PCA)

PCA is a statistical procedure that uses an orthogonal transformation to transform a set of possibly notice correlated variables into a set of linearly uncorrelated variables called principal components. The number of principal components is less than or equal to the number of original variables.

This technique is indicated for reducing the number of variables in a data set without loss of information and as possible as produce more meaningful variables because it cannot usually easy to interpret. Data reduction considers the most important feature that made PCA is applied successfully in image compression, but in many applications PCA is used only to introduce information on the correct dimensionality of a data set.

[Berg et al., 1994],have presented a new multiple source eye correction (MSEC) approach of eye artifact treatment based on multiple source analysis. Principal Component Analysis (PCA) method requires a precise modeling of propagation ways for the included signals. Output results have displayed that PCA method cannot perfectly separate ocular artifact from EEG, when both the waveforms have similar voltage magnitudes. [Lagerlund et al., 1997], have presented PCA with Singular Value Decomposition (SVD) for spatial filtering of multichannel ECG. This method needs the distribution of the signal sources to be orthogonal while its performance is finite to decorrelating signals, so it cannot treat with higher-order statistical dependencies.

PCA works by transforming a set of correlated variables into a new set of uncorrelated variables that are named the principal components. While, if the variables in a data set are already uncorrelated then PCA is of no value i.e. uncorrelated and the principal components are orthogonal and are ordered in expression of the variability they represent. So for a single dimension or variable, the first principle component represents the largest amount of variability in the original data set.

The PCA operation can be performed in different methods, but the most straightforward one is a geometrical interpretation. While PCA is applicable to data sets containing any number of variables, it is simpler to describe using only two variables since this leads to easily visualized graphs.

Independent Component Analysis (ICA)

PCA shows that the uncorrelated data is not enough to output independence variables at least when the variables have nongaussian distributions.

ICA is a computational method for separating a multivariate signal into collective subcomponents. These subcomponents are assumed to be non-Gaussian signals and statistically independent from each other.

The purpose of ICA is to transform the original data set into number of independent variables in order to detect more meaningful variables and not to minimize the dimensionality of the data set; but when data set minimization is also required,PCA is used for preprocessing the data set.This problem is shown in biosignal processing like EEG signals when a combination between the underlying neural sources in the head and EEG signal itself.

The main computational difference between ICA and PCA is that PCA uses only second order statistics while ICA uses higher order statistics.

Most signals do not have a Gaussian distribution so they have higher-order moments while variables with a Gaussian distribution have zero statistical moments higher than second order,for this the higher order statistical properties are good analysis in ICA.

While the similarity between ICA and PCA is in the component’s determination thatinitiate by eliminatingthe mean values of the variables which is called centering the data, then whiten the data which is termed sphering the data. These whitened data are uncorrelated but all the components have unit variances.

ICA necessarily to meet two conditions: the source variables must be independent and non-Gaussian (not need the distribution of the source variables to beknown)and these two conditions are work together when the sources are real signals. While third limitation is that the mixing matrix must be square i.e. the number of sources should equal the number of measured signals, but it is not real limitation because PCA can be applied to minimize the dimension of the data set in order to be equal to the source data set.

[Comon, 1994], has presented ICA which is an expansion of PCA. It not only decorrelates but can also treat with higher order statistical dependencies. [Lee et al., 1996],have used Infomax (an optimization principle for artificial neural networks).[Vigário, 1997], has introduced ICA for extracting of EOG signal from EEG recording. Extended Infomax which was the most popular ICA algorithms for denoising EEG, as well as JADE (JointApproximation Diagonalisation of Eigen Matrices which is another signal source separation technique) that have been used by [Cardoso, 1998]. [Vigon et al., 2000], have made quantitative evaluation of different techniques used for ocular artifact cancellation in EEG signals. The obtained results showed that the signal separation techniques of JADE and extended ICA are more efficacious than EOG subtraction and PCA for filtering ocular artifact from the EEG waveforms. In the same year, [Jung et al., 2000],have presented the successful application of ICA for removing EEG artifacts, the results showed that a number of different artifacts have been cancelled and separated successfully from EEG and magnet oencephalogram (MEG) recordings. The disadvantages of this method are firstly, visual examination of the acquired sources wanted to carry out artifact removing and secondly, there is undesirable data loss in the conditions where complete trials are removed.

[Hyung-Min Park et al., 2002], have proposed ANC based on Independent Component Analysis (ICA) by using higher-order statistics.[Nicolaou et al., 2004], have proposed the application of TDSEP (Temporal Decorrelation Source Separation which is a specific extension of ICA) for automatic artifact removal from EEG signals. This analysis has an advantage of separating signals with Gaussian amplitude distribution (because separation is based on the correlation of the sources).[Azzerboni et al., 2004],have proposed a method that used wavelet transform and ICA combination for removing the artifacts in surface EMG, according to this study, the author found that in order to identify the artifact user interface is needed.[Yong Hu et al., 2005], have introduced a denoising method using ICA and a HPF for removing the ECG interference in SEMG recorded from trunk muscles.

In biomedical image processing, ICA has been used to uncover active neural areas in functional magnetic resonance imaging by estimating the underlying neural sources in EEG signal and to detect the underlying neural control components in an eye movement motor control system.

One of the most important applications of PCA and ICA is their ability to search for components related to blood flow dynamics or artifacts during Functional Magnetic Resonance Imaging (fMRI).FMRI is a technique for measuring brain activity and has become a major tool to image human brain function by detecting the changes in blood oxygenation and flow that occur in response to neural activity.The development of FMRI in the 1990s and became one of the most popular neuroimaging methods which mostly attributed to Seiji Ogawa and Ken Kwong.The application of PCA and ICA on fMRI image has a rectangle active area (Fig.18)to recognize the artifact and signal components in a region with active neurons shown in Fig. 19-20. The pattern results by using ICA shown in Fig.19 are better separated than the results shown in Fig.20 usingPCA.

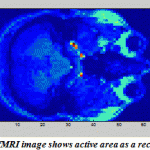Figure.18:fMRI image shows active area as a rectangle Click here to view full figure

 

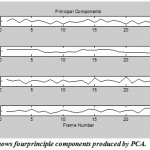Figure.19: shows fourprinciple components produced by PCA Click here to view full figure

 

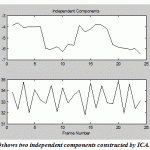Figure.20: shows two independent components constructed by ICA Click here to view full figure

Fmri Parcellation

To obtain the best performance for whole brain functional connectivity data analysis, the brain must be divided into ROIs to be used as network nodes. The structures of ROIs are normally at the level of many voxels constituting which a possibly small brain region, and rarely at the level of a specific voxel. Several methods have been proposed for defining ROIs and study function beyond the voxel description, which include using three strategies: (1) Randomly splitting the brain into anatomical or functional regions of interest (ROIs), (2) Anatomical brain atlas, (3) Brain parcellations using data-driven or clustering functional data.

For randomly splitting the brain into ROIs, the selection of these regions is depended on background and long experiments because of the cancellation problem, so any signal lies outside the ROI will be ignored as a consequence and the final results will not fit perfectly the new data. Therefore, this is regarded as a limitation by using the first strategy for defining ROIs.

The anatomical brain atlas provides a set of ROIs that cover all the brain volume [Mazziotta et al., 2001; Tzourio-Mazoyer et al., 2002; Shattuck et al., 2008] or structures (anatomically, functionally or based on connectivity). There are two limitations by using the brain atlases: (1) All brain atlases are inconsistent between them [Bohland et al., 2009], (2) Each atlas may not perfectly fit the data.

Brain parcellations are either anatomical or functional parcellations. The parcels in anatomical parcellations these parcels must be performed with the most appropriate atlas, while the functional parcellations can be derived either from resting-state functional Magnetic Resonance Images (rs-fMRIs), activation data or other analyses; and functional parcellations use data-driven or clustering functional data.

Parcellation approaches use brain activity and clustering approaches to divide the brain into many parcels or regions with some degree of homogeneous characteristics. So, the brain is divided into define regions with some degree of signal homogeneity that help for analysis and interpretation of neuroimaging data as well as mining these data because of the amount of fMRI data are huge.

Parcellation with BOLD Shape

Parcellation method is another approach that used for fMRI data analysis; it is used to overcome the mis-registration problem and dealing with the limitation of spatial normalization. As we explained previously that there are either anatomical or functional parcellations, the most important area of neuroscience is functionally parcellation of the human cerebral cortex. Parcellation of the human brain has been done by Brodmann in early 20th century, based on the brain cytoarchitecture and divided it into 52 different fields.

1. Flandin et al., (2002), they have used a brain parcellation technique to overcome the shortcomings of spatial normalization for model-driven fMRI data analysis. By using GLM parameters and group analysis, they functionally parcellate the brain of each subject into about 1000 homogenous parcels.
2. Thirion et al., (2006), they have used a multi-subject whole brain parcellation technique to overcome the shortcomings of spatial normalization of fMRI datasets. By using GLM parameters analysis, they parcellate the whole brain into a certain number of parcels. They collected voxels from all subjects together, and then derived parcel prototypes by using C-means clustering algorithm on GLM parameters.

Parcellation Based on a Data Driven Approach

Data-driven analysis is widely used for fMRI data processing to overcome the limitation associated with the shape of the Hemodynamic Response Function (HRF) and task-related signal changes that must be introduced. As well as the assumption about the shapes of BOLD model, there is another limitation related to the subject behavior during the task. So data-driven analysis is used with parcellation technique for fMRI data processing, in which the detection of brain activation is obtains from the information of the fMRI signal only.

1. Yongnan Ji et al., (2009), they have introduced a parcellation approach for fMRI datasets based on Independent Component Analysis (ICA) and Partial Least Squares (PLS) instead of the GLM, and they used a spectral clustering of the PLS latent variables to parcellate all subjects data.
2. Thomas B. et al., (2013), they have proposed a novel computational strategy to divide the cerebral cortex into disjoint, spatially neighboring and functionally homogeneous parcels using hierarchical clustering parcellation of the brain with resting-state fMRI.
3. Thirion B. et al., (2014), they have studied the criteria accuracy of fit and reproducibility of the parcellation across boot strap samples on both simulated and two task-based fMRI datasets for the Ward, spectral and k-means clustering algorithms. They have addressed the question of which clustering technique is appropriate and how to optimize the corresponding model. The experimental results show that Ward’s clustering performance was the best among the alternative clustering methods.

Conclusion

DSP techniques deals with processing signals in digital domain which can be used for removing noise as well as adjusting signal characteristics, spectral estimation, multiplying two signals to perform modulation or correlation, Filtering and averaging.

ECG, EEG, EMG, ERG, EOG and others are examples of the biosignals, and all these biosignals have been tested in the frequency domain. There are many applications of signal processing in biomedical field to perform different techniques: Echo cancellation, Noise cancellation, Spectrum Analysis, Detection, Correlation, Filters, Computer Graphics, Image Processing, Data Compression, Machine vision, Sonar, Array Processing, Guidance, robotics and etc.

From this paper we conclude that there is a growing interest and motivation in using digital signal processing techniques with biosignals like ECG, EEG and EMG, e.g., the majority of the literature reviewed in this paper were published within recent years.

From second part of this article we conclude that in spite of brain atlases obvious usefulness, but existing atlases are limited due to the inconsistently and may not fit the data well.

Unlike brain atlases, data-driven parcellations that used to define regions of interest can be derived from various image modalities reflecting different neurobiological information.

As well as the most popular parcellation techniques that are depend on the assumption about the shapes of BOLD model or the subject behavior during the task,parcellations can also be obtained from data-driven analysis such as independent components analysis (ICA) and variants of principal components analysis (PCA) which rely on a linear mixing approach that changes the nature of the problem and implies other probabilistic models.

This work is of vital important for researcher who wants to learn about DSP applications with biomedical signals as well as it consider as a good starting for researcher who areinteresting in fMRI brain activation extractions techniques.In future, this work can be extended so introduce some results related to fMRI parcellation approach deals with resting-state data or task data.

Refrences

1. Abboud S., Sadeh D., “Spectral analysis of the fetal electrocardiogram”, Computers in Biology and Medicine, Vol.19, No.6, pp.409-415, (1989).
2. Akkiraju P., Reddy D.C., “Adaptive cancellation technique in processing myoelectric activity of respiratory muscles”, IEEE Transactions on Biomedical Engineering, Vol.39, No.6, pp.652-655, (1992).
3. Aldroubi A., Unser M., “Wavelets in Medicine and Biology”, CRC Press, Boca Raton, FL, (1996).
4. Azzerboni B., Carpentieri M., La Foresta F., Morabito F.C., “Neural-ICA and wavelet transform for artifacts removal in surface EMG”, IEEE International Joint Conference on Neural Networks, Vol.4, pp.3223-3228, (2004).
5. Beckmann C. and Smith S., “Probabilistic independent component analysis for functional magnetic resonance imaging”, Medical Imaging, IEEE Transactions on Medical Imaging, 23 (2), 137–152, (2004).
6. Benjamin Friedlander, “System identification techniques for adaptive noise canceling”, IEEE Transactions on Acoustics, Speech and Signal Processing, Vol.30, No.5, pp.699-709, (1982).
7. Berg P., Scherg M., “A multiple source approach to the correction of eye artifacts”, Electroencephalography and Clinical Neurophysiology Vol.90, No.3, pp.229-241, (1994).
8. Boashash B., “Time-Frequency Signal Analysis”, Longman Cheshire Pty Ltd., (1992).
9. Boashash B., Black, P.J., “An efficient real-time implementation of the Wigner-Ville Distribution”, IEEE Trans. Acoust. Speech Sig. Proc. ASSP-35:1611–1618, (1987).
10. Bohland J. W., Bokil H., Allen C. B., Mitra P. P., “The brain atlas concordance problem: quantitative comparison of anatomical parcellations”, PLoS ONE 4:e7200, (2009).
11. Boudreaux-Bartels G. F., Murry R., “Time-frequency signal representations for biomedical signals”, In: The Biomedical Engineering Handbook. J. Bronzino (ed.) CRC Press, Boca Raton, Florida and IEEE Press, Piscataway, N.J., (1995).
12. Browne M., Cutmore T.R.H., “Low probability event-detection and separation via statistical wavelet thresholding: An application to psychophysiological de-noising”, In Clinical Neurophysiology, Vol.113, No.9, pp.1403-1411, (2002).
13. Cardoso J.F., “Blind signal separation: statistical principles”, IEEE Proceedings (Special Issue on blind identification and estimation), Vol.90, No.8, pp.2009-2026, (1998).
14. Chen J.D.Z., Lin Z.Y., Ramahi M., Mittal R.K., “Adaptive cancellation of ECG artifacts in the diaphragm electromyographic signals obtained through intraesophageal electrodes during swallowing and inspiration”, Neurogastroenterology and Motility, Vol.6, pp.279-288, (1994).
15. Cohen L., “Time-frequency distributions—A review”, Proc. IEEE 77:941–981, (1989).
16. Comon P., “Independent component analysis, a new concept?”, Special issue on Higher-Order Statistics, Vol.36, No.3, pp.287-314, (1994).
17. Conforto S., D’Alessio T., Pignatelli S., “Optimal rejection of movement artifacts from myoelectric signals by means of a wavelet filtering procedure”, Journal of Electromyography and Kinesiology, Vol.9, No.1, pp.47-57, (1999).
18. Echeverria J.C., Ramirez N., Pimentel A.B., Rodriguez R.,Gonzalez R., Medina V., “Fetal QRS extraction based on wavelet analysis and pattern matching”, Proceedings of IEEE on Engineering in Medicine and Biology Society, Vol.4, pp.1656-1657, (1996).
19. Echeverria J.C., Ortiz R., Ramirez N., Medina V., Gonzalez R., “A reliable method for abdominal ECG signal processing”, Computers in Cardiology, Vol.25, pp.529-532, (1998).
20. Fergjallah M., Barr R.E., “Frequency-domain digital filtering techniques for the removal of power-line noise with application to the electrocardiogram”, Computers in Biomedical Research, Vol.23, pp.473-489, (1990).
21. Ferrara E., Widrow B., “Fetal Electrocardiogram enhancement by time-sequenced adaptive filtering”, IEEE Trans. Biomed. Engr. BME-29:458–459, (1982).
22. Flandin, G., Kherif, F., Pennec, X., Malandain, G., Ayache, N., Poline, J.-B., “Improved detection sensitivity in functional mri data using a brain parcelling technique”, in: Dohi, T., Kikinis, R. (Eds.), MICCAI (1). Vol. 2488 of Lecture Notes in Computer Science, Springer, pp. 467–474, (2002).
23. Glover J.R., “Adaptive noise canceling applied to sinusoidal interferences”, IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol.ASSP-25, No.6, pp.484-491, (1977).
24. Grieve R., Parker P.A., Hudgins B., Englehart K., “Nonlinear adaptive filtering of stimulus artifact”, IEEE Transactions on Biomedical Engineering, Vol.47, No.3, pp.389-395, (2000).
25. Griffiths L.J., “An adaptive lattice structure for noise canceling applications”, Proceedings of IEEE International Conference on Acoustic, Speech, Signal Processing, Tulsa, pp.87-90, (1978).
26. Grujic T., Kuzmanic A., “Denoising of surface EMG signals: A comparison of wavelet and classical digital filtering procedures”, Healthcare Technology, Vol.12, No. 2, pp. 130-135, (2004).
27. Hae-Jeong Park, Do-Un Jeong, Kwang-Suk Park, “Automated detection and elimination of periodic ECG artifacts in EEG using the energy interval histogram Method”, IEEE Transactions on Biomedical Engineering, Vol.49, No.12, pp.1526-1533, (2002).
28. Haykin S., “Adaptive Filter Theory,2nd ed.”, Prentice-Hall, Inc., Englewood Cliffs, N.J., (1991).
29. He P., Wilson G., Russell C., “Removal of ocular artifacts from electroencephalogram by adaptive filtering”, Medical and Biological Engineering and Computing, Vol. 42, No.3, pp. 407-412, (2004).
30. Hee-Kyoung Park, Seong-Gon Kong, “Neuro-fuzzy control system for adaptive noise cancellation”, IEEE Conference Proceedings on Fuzzy Systems, Vol.3, pp.1465-1469, (1999).
31. Huhta J.C., Webster J.G., “60-Hz Interference in Electrocardiography”, IEEE Transactions on Biomedical Engineering, Vol.20, No.2, pp.91-101, (1973).
32. Hyung-Min Park, Sang-Hoon Oh, Soo-Young Lee, “On adaptive noise cancelling based on independent component analysis”, Electronics Letters, Vol.38, No.15, pp.832-833, (2002).
33. Inan Güler, Elif Derya Übeyli, “Application of adaptive neuro-fuzzy inference system for detection of electrocardiographic changes in patients with partial epilepsy using feature extraction”, Expert Systems with Applications, Vol.27, No.3, pp.323-330, (2004).
34. Ingle V.K., Proakis J. G., “Digital Signal Processing with MATLAB”, Brooks/Cole, Inc. Pacific Grove, CA, (2000).
35. Jafari M.G., Chambers J.A., “Fetal electrocardiogram extraction by sequential source separation in the wavelet Domain”, IEEE Transactions on Biomedical Engineering, Vol.52, No.3, pp.390- 400, (2005).
36. John L. Semmlow, “Biosignal and Biomedical Image Processing: MATLAB Based Applications”, Marcel Dekker Inc., (2004).
37. Joonwan Kim, Poularikas A.D., “Comparison of two proposed methods in adaptive noise canceling”, Proceedings 35th Southeastern Symposium on System Theory, pp.400-403, (2003).
38. Jung T.P, Makeig S., Humphries C., Lee Te-Won, Mckeown M.J., Iragui V., Sejnowski T.J., “Removing electroencephalographic artifacts by blind source separation”, Phychophysiology, Vol.37, pp.163-178, (2000).
39. Khamene A., Negahdaripour S., “A new method for the extraction of fetal ECG from the composite abdominal Signal”, IEEE Transactions on Biomedical Engineering, Vol.47, No.4, pp.507-516, (2000).
40. Koford J., Groner G., “The use of an adaptive threshold element to design a linear optimal pattern classifier”, IEEE Transactions on Information Theory, Vol.12, No.1, pp.42-50, (1966).
41. Lagerlund T.D., Sharbrough F.W., Busacker N.E., “Spatial filtering of multichannel electroencephalographic recordings through principal component analysis by singular value decomposition”, Clinical Neurophysiology, Vol.14, No.1, pp.73-82, (1997).
42. Lee T.W., Sejnowski T., “Independent component analysis for sub gaussian and super-gaussian mixtures”, Proceedings of 4th Joint Symposium on Neural Computation, Vol.7, pp.132-139, (1996).
43. Levine S., Gillen J., Weiser P., Gillen M., Kwatny E., “Description and validation of an ECG removal procedure for EMGdi power spectrum analysis”, Journal of Applied Physiology, Vol.60, No.3, pp.1073-1081, (1986).
44. Marple S.L., “Digital Spectral Analysis with Applications”, Prentice-Hall, Englewood Cliffs, NJ, (1987).
45. Marque C., Bisch C., Dantas R., Elayoubi S., Brosse V., Perot C., “Adaptive filtering for ECG rejection from surface EMG recordings”, Journal of Electromyography and Kinesiology, Vol.15, pp.310-315, (2005).
46. Martens S.M.M., Bergmans J.W.M., Oei S.G., “A simple adaptive interference cancellation method for power line reduction in electrocardiography”, Proceedings of the 25th Symposium on Information Theory in the Benelux, pp.49-56, (2004).
47. Martens S.M.M., Mischi M., Oei, S.G., Bergmans J.W.M., “An improved adaptive power line interference canceller for electrocardiography”, IEEE Transaction on Biomedical Engineering, Vol.53, pp.2220-2231, (2006).
48. Mazziotta, J., Toga, A., Evans, A., Fox, P., Lancaster, J., Zilles, K., et al., “A probabilistic atlas and reference system for the human brain: international consortium for brain mapping (icbm)”, Philos. Trans. R. Soc. Lond. B Biol. Sci. 356, 1293–1322, (2001).
49. Mochimaru F., Fujimoto Y., Ishikawa Y., “Detecting the fetal electrocardiogram by wavelet theory-based Methods”, Progress in Biomedical Research, Vol.7, No.3, pp.185-193, (2002).
50. Ng E.Y.K., Fok S.C., Peh Y.C., Ng F.C., Sim L.S.J., “Computerized detectionof breast cancer with artificial intelligenceand thermograms”, International Journal ofMedical Engineering and Technology, Vol.26, No. 4, pp. 152-157, (2002).
51. Nicolaou N., Nasuto S.J., “Temporal independent component analysis for automatic artefact removal from EEG”, MEDSIP 2004, 2nd International Conference on Medical Signal and Information Processing, Malta, pp.5-8, (2004).
52. Outram N.J., Ifeachor E.C., Van P.W.J., Eetvelt, Curnow J.S.H., “Techniques for optimal enhancement and feature extraction of fetal electrocardiogram”, IEEE Proceedings of Science and Measurement Technology, Vol.142, No.6, pp.482-489, (1995).
53. Park Y.C. Cho, Kim B.M., Kim N.H., Park W.K., Youn S.H., Yonsei D.H., “A fetal ECG signal monitoring system using digital signal processor”, IEEE International Symposium on Circuits and Systems, Vol.3, pp.2391-2394, (1988).
54. Ping Zhou, Lowery M.M., Weir R.F., Kuiken T.A., “Elimination of ECG artifacts from myoelectric prosthesis control signals developed by targeted muscle reinnervation”, 27th Annual International Conference of the Engineering in Medicine and Biology Society, IEEE-EMBS, pp.5276-5279, (2005).
55. Rao R.M., Bopardikar A.S., “Wavelet Transforms: Introduction to Theory and Applications”, Addison-Wesley, Inc., Reading, MA, (1998).
56. Selvan S., Srinivasan R., “Removal of ocular artifacts from EEG using an efficient neural network based adaptive filtering technique”, IEEE Signal Processing Letters, Vol.6, No.12, pp.330-332, (1999).
57. Shattuck, D. W., Mirza, M., Adisetiyo, V., Hojatkashani, C., Salamon, G., Narr, K. L., et al., “Construction of a 3d probabilistic atlas of human cortical structures”, Neuroimage 39, 1064–1080, (2008).
58. Shiavi R., “Introduction to Applied Statistical Signal Analysis, 2nd ed.”, Academic Press, San Diego, CA, (1999).
59. Stearns S.D., David R.A., “Signal Processing Algorithms in MATLAB”, Prentice Hall, Upper Saddle River, NJ, (1996).
60. Strang G., Nguyen T., “Wavelets and Filter Banks”, Wellesley-Cambridge Press, Wellesley, MA, (1997).
61. Suzuki A., Sumi C., Nakayama K., Mori M., “Real-time adaptive cancelling of ambient noise in lung sound Measurements”, Medical and Biological Engineering and Computing, Vol.33, No.5, pp.704-708, (1995).
62. Tatjana Zikov, Stephane Bibian, Guy A. Dumont, Mihai Huzmezan, “A wavelet based de-noising technique for ocular artifact correction of the electroencephalogram”, Proceedings of the Second Joint EMBS/BMES Conference, Vol.1, pp.98-105, (2002).
63. Thirion B., Flandin G., Pinel P., Roche A., Ciuciu P., Poline J.-B., “Dealing with the shortcomings of spatial normalization: multi-subject parcellation of fMRI datasets”, Human brain mapping 27, 678–693, pMID: 16281292, Wiley-Liss, Inc., (2006).
64. Thirion B., Gaël V., Elvis D., Jean-Baptiste P., “Which fMRI clustering gives good brain parcellations?”, Frontiers in Neuroscience, Article167, Volume8, (2014).
65. Thomas B., Saad J., Matthew F.G., David C.V.E., Kamil U., Timothy E. J. B., Stephen M.S., “Spatially constrained hierarchical parcellation of the brain with resting-state fMRI”, Neuroimage; 76:313-24, (2013).
66. Tzourio-Mazoyer N., Landeau B., Papathanassiou D., Crivello F., Etard O., Delcroix N., Mazoyer B., Joliot M., “Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain”, Neuroimage, 15(1): 273–89, (2002).
67. Vigário R.N., “Extraction of ocular artefacts from EEG using independent component analysis”, Electroencephalography and Clinical Neurophysiology, Vol.103, No.3, pp.395-404, (1997).
68. Vigon L., Saatchi M. R., Mayhew J.E.W., Fernandes R., “Quantitative evaluation of techniques for ocular artifact filtering of EEG waveforms”, in IEEE Proceedings of Science and Measurement Technology, Vol.147, No.5, pp.219-228, (2000).
69. Wickerhauser M.V., “Adapted Wavelet Analysis from Theory to Software”, A.K. Peters, Ltd. and IEEE Press, Wellesley, MA, (1994).
70. Widrow B., Hoff M.E., “Adaptive switching circuits’, In IRE WESCON Convention Record, pp.96-104, New York, (1960).
71. Widrow B., Glover J.R., McCool J.M., Kaunitz J., Williams C.S., Hearn R.H., Zeidler J.R., Eugene Dong, Goodlin R.C., “Adaptive noise cancellation: Principles and applications”, IEEE Proceedings, Vol.63, No.12, pp.1692-1716, (1975).
72. Widrow B., McCool J.M., Larimore M.G., Johnson C.R., “Stationary and nonstationary learning characteristics of the LMS adaptive filter”, IEEE Proceedings, Vol.64, pp.1151-1162, (1976a).
73. Widrow B., McCool J.M., “A comparison of adaptive algorithms based on the methods of steepest descent and random search”, IEEE Transaction Antennas Propagation, Vol.24, No.5, pp.615-637, (1976b).
74. Widrow B., Stearns D., “Adaptive Signal Processing”, Prentice Hall, Upper Saddle River, NMJ, (1985).
75. Widrow B., Winter R., “Neural nets for adaptive filtering and adaptive pattern recognition”, IEEE Proceedings on Computer, Vol.21, No.3, pp.25-39, (1988).
76. Ye Datian, Ouyang Xuemei, “Application of wavelet analysis in detection of fetal ECG”, Proceedings of IEEE Engineering in Medicine and Biology Society, Vol.3, pp.1043-1044, (1996).
77. Yilmaz A., English M.J., “Adaptive non-linear filtering of ECG signals: dynamic neural network approach”, IEEE Colloquium on Artificial Intelligence Methods for Biomedical Data Processing, No.26, pp.1-6, (1996).
78. Yin H., Eng Y., Zhang J., Pan Y., “Application of adaptive noise cancellation with neural network based fuzzy inference system for visual evoked potentials estimation”, Physics and Engineering in Medicine, Vol.26, No.1, pp.87-92, (2004).
79. Yongnan Ji, Pierre-Yves H., Uwe A., Alain P., “Parcellation of fMRI datasets with ICA and PLS- a data driven approach”, MICCAI 2009, part I, LNCS 5761, pp 984-991, by Springer Berlin Heidelberg, (2009).
80. Yong Hu, Li X.H., Xie X.B., Pang L.Y., Yuzhen Cao, Kdk Luk, “Applying independent component analysis on ECG cancellation technique for the surface recording of trunk Electromyography”, IEEE-EMBS 2005 27th Annual International Conference of the Engineering in Medicine and Biology Society, Issue 01-04, pp.3647-3649, (2005).
81. Zarzoso V., Nandi A.K., “Noninvasive fetal electrocardiogram extraction: blind separation versus adaptive noise cancellation”, IEEE Transactions on Biomedical Engineering, Vol.48, No.1, pp.12-18, (2001).
82. Ziarani A.K., Konrad A., “A nonlinear adaptive method of elimination of power line interference in ECG signals”, IEEE Transaction on Biomedical Engineering, Vol.49, pp.540-547, (2002).

 

 

 

(Visited 1,309 times, 1 visits today)